Parallel Query Processing
Relevant Materials #
Parallelism #
Parallelism helps us break down a big problem into small, independent chunks. The idea is that a lot of machines all working on the same problem at the same time will finish the problem more quickly.
There are two main metrics we want:
- Speed-up: if we add more hardware, the same workload should be completed more quickly.
- Scale-up: if the workload increases, we should be able to add a corresponding amount of hardware to make the problem be processed with the same amount of time as before.
There are two main types of parallelism:
- Pipelining: each machine does one component of the calculation, then passes the result on to another machine
- Partitioning: each machine runs the same computations on a different set of data.
Now for types of query parallelism:
- Inter-query parallelism: each query runs on a different processor. Requires parallel-aware concurrency control.
- Intra-query, inter-operator parallelism: each operator in one query is done by a differerent machine.
- Pipeline parallelism: every query operation depends on the previous query’s output
- Bushy tree parallelism: do two operators at the same time if they don’t depend on each other
- Intra-query, intra-operator parallelism: for joins, each machine scans and processes a chunk of the table, and all results are eventually combined.
- Partition parallelism: partition the data, and operate on each partition simultaneously since they don’t depend on each other
Data Partitioning #
So, if we’re going to do intra-operator parallelism, how do we split up the data in the first place?
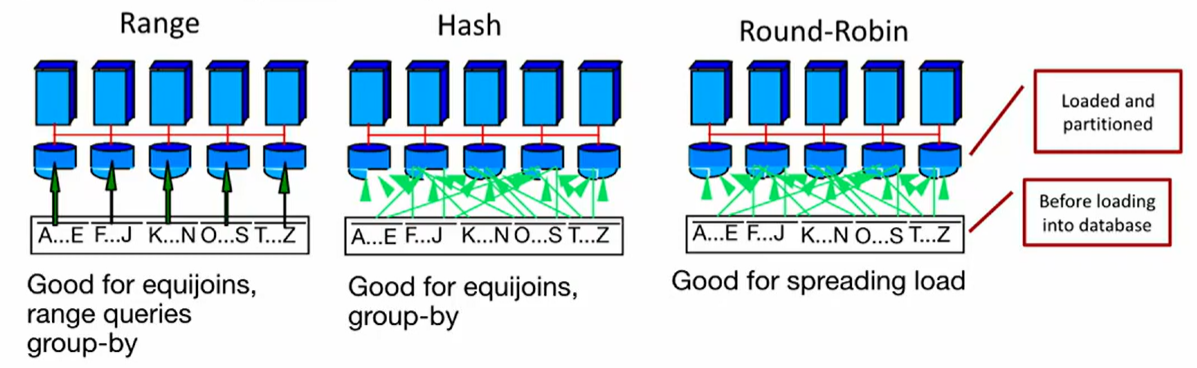
Range and hash partitioning are prone to key-skew. Round-robin ensures that all machines receive roughly equal amounts of work regardless of the data distribution.
However, with range and hash partitioning, searching is more efficient since we only need to query a subset of machines.
Parallel Query Operators #
Parallel Hashing #
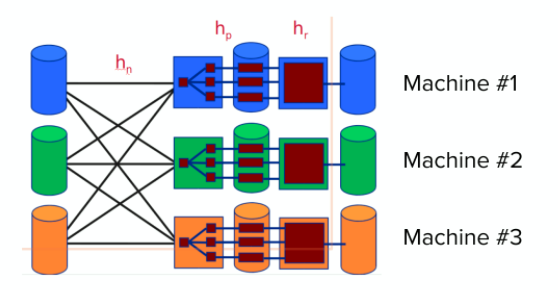
Add a new partitioning phase to separate data into machines before running the algorithm individually for each machine.
Parallel Hash Joins #
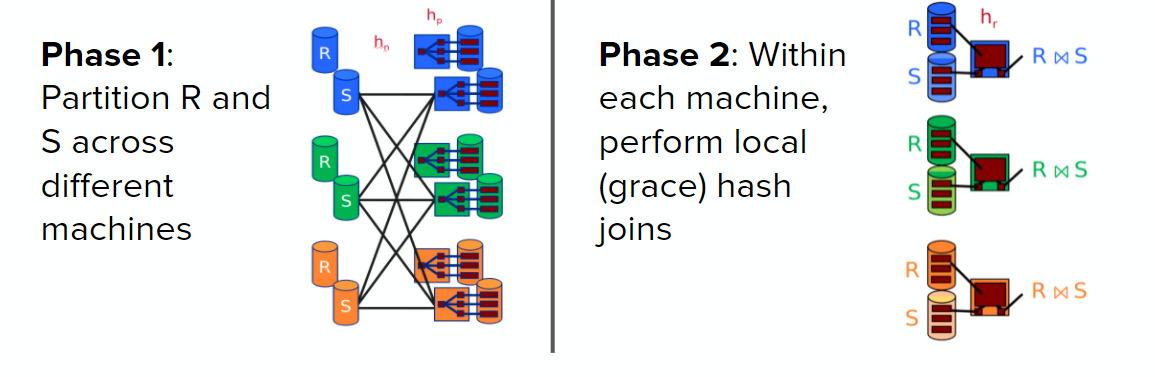
Use hash partitioning on both relations, then perform a normal hash join on each machine independently.
Symmetric Hash Joins #
Symmetric hash joins are a type of streaming hash join algorithm: it does not require all tuples to be available when it runs.
Basic idea: build two hash tables ($R$ and $S$) at the same time
- When a tuple from $R$ arrives, probe hash table for $S$ and add the tuple into hash table for $R$.
- If there are matching tuples in $S$, then add all joined tuples to the output by iterating over the hash table bucket.
- Do the same for $S$ and $R$.
Parallel Sorting #
Partition the data over machines using range partitioning. Then, perform sort-merge join independently on each machine. Since each range is independent, we can join all of them at the end for the final output.
Parallel Hashing #
Parallel hashing uses the same idea as parallel sorting, except that since we don’t care about sort order we use hash partitioning instead.
Parallel Aggregation #
SUM, COUNT, AVERaGE, etc.
- Use hierarchical aggregation: first, local function calculates sum and count for both machines. Then, a global function combines the results from all of the machines.
Asymmetric Shuffles #
Sometimes, data is already partitioned the way we want. This would make it redundant to repartition or send data.
For example, if we wanted to run sort-merge join on R and S, but R is already range partitioned, then we can leave R alone and range-partition S using the same ranges before performing the merge.
Broadcast Joins #
Sometimes, one table is tiny and another one is huge. It can be very expensive to partition the huge table, so we can instead send the entire tiny table to each machine containing the huge table and perform the operation locally.
Here are some examples of parallel operations:
- Lookup by key: easy for range/hash, need to broadcast to all machines for RR
- Insert: need specific machine for range/hash, can go to any machine for RR
- Unique key: easy for range/hash, need to broadcast request for RR. If response received, overwrite in correct machine. Otherwise, insert anywhere
Measuring Parallelism (Problem solving strategies) #
Network cost: amount of data we need to send over the network to perform an operation
- Measured in bytes/KB/GB etc.
- Unlike I/Os, we can send one tuple at a time rather than entire pages
- Network cost is incurred whenever a tuple needs to be moved to another machine (e.g. due to partitioning). Typically all data originates on 1 of the machines and needs to be distributed.
Measuring partitioning costs:
- Given $N$ pages on one machine, we want to partition the data onto $M$ machines. How much data would be transferred if each page is $S$ KB large?
- If all data is uniform and hash functions are uniformly distributed, all partition schemes (hash, range, RR) would put $N/M$ pages on each machine. $M-1$ machines need to be written to, so $\frac{N}{M} \times (M-1) \times S$ KB would be written.
- In the best case, range and hash partitioning would not need to write anything at all (since everything is on the first machine). So the cost is $0$ KB. Round Robin best case is the same as the above calculation.
- In the worst case, range and hash partitioning would need to write all $M$ pages to other machines, so $M \times S$ KB would be written. Round Robin is guaranteed to always uniformly distribute data so its worst case and best case are the same.