Binary Trees

 

“The most important concept in computer science” - Josh Hug

Humble Origins #

Linked lists are great, but we can do better! Let’s try rearranging the pointers in an interesting way.

Instead of starting at one end of the list, let’s set our first pointer at the middle of the list!

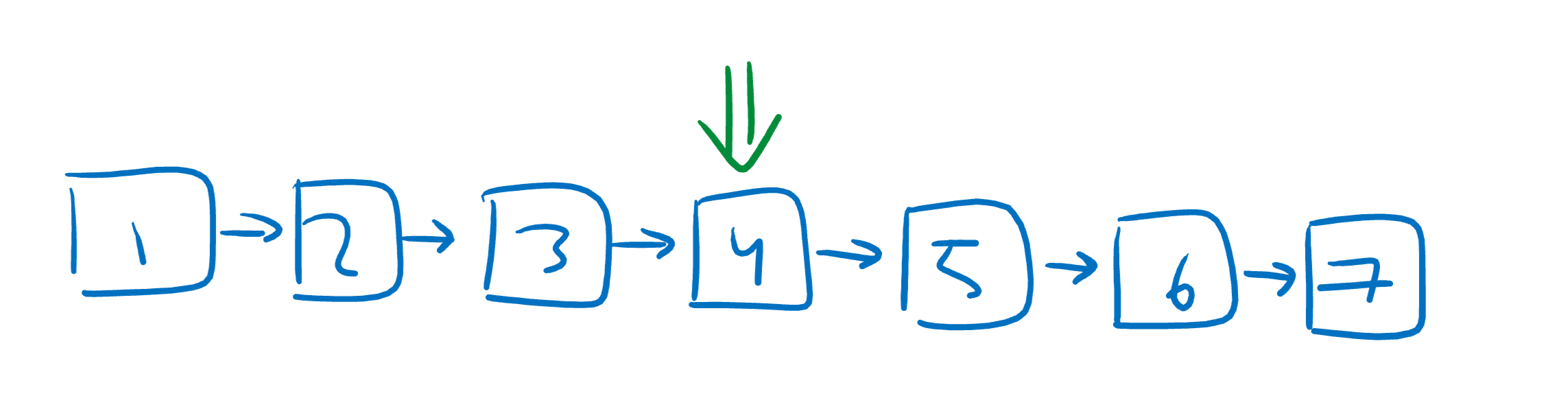
Now, let’s make new pointers going to the center of each sublist on the left and right of the center.

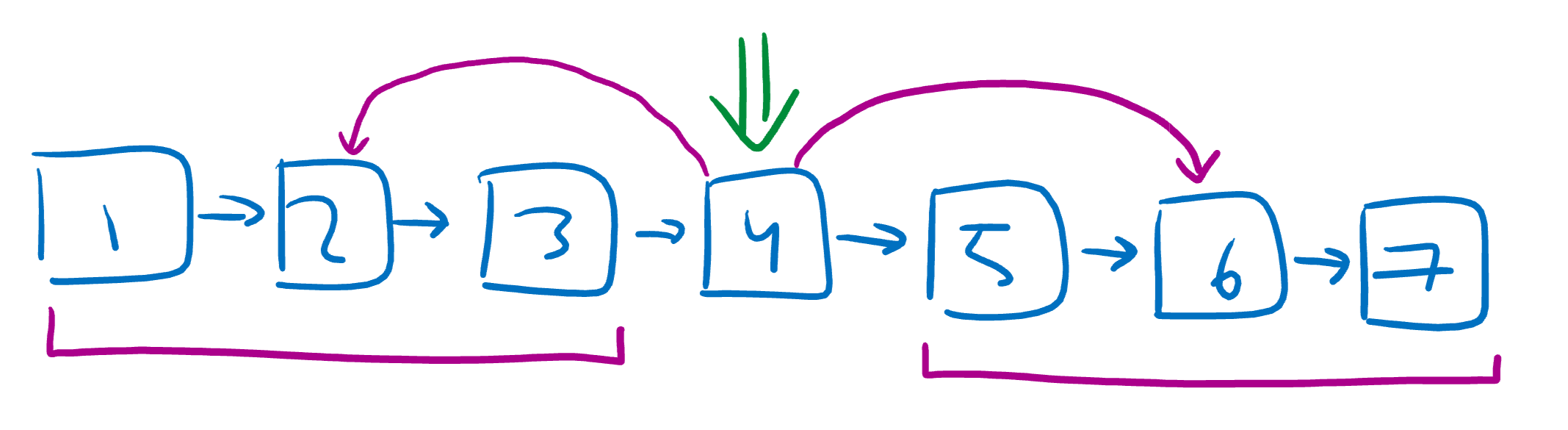
Let’s do it again!

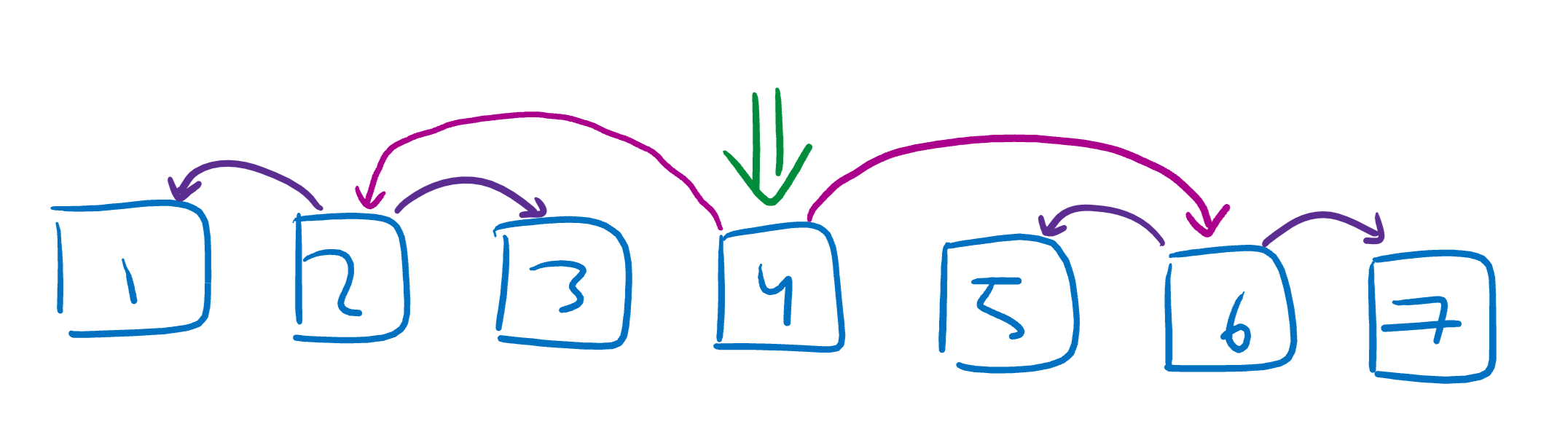
Would ya look at that, we’ve got a tree! 🌲

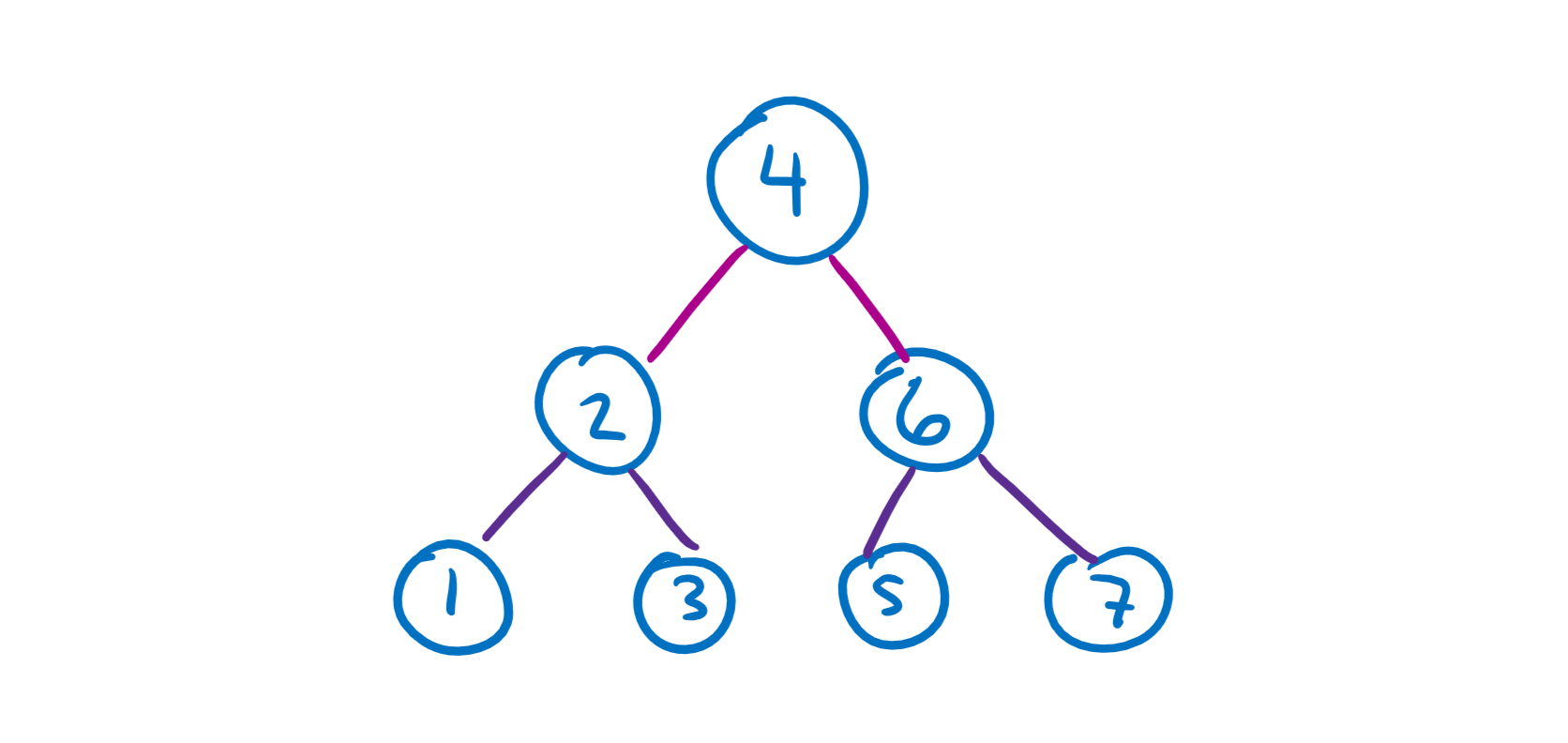
Types of Trees #

Right now, we can determine some properties that all trees have.

• All trees have a root node.
• All nodes can point to child nodes. Or, if they don’t have any children, they are leaves.

We can add more and more constraints to our tree to make them more useful!

First, let’s add the constraint that node can only have 2 or fewer children to create a binary tree.

Then, let’s ensure our tree is sorted to create a binary search tree. A tree is sorted if it has these properties:

• Every value in the left subtree of a node is less than the node’s value.
• Every value in the right subtree of a node is greater than the node’s value.
• Values are transitive - there are no duplicate values.
• The tree is complete - it is possible to compare any two values in the tree and say that one is either less than or greater than the other.
• The tree is antisymmetric - If p < q is true and q < r is also true, then it must follow that p < r.

Tree Operations #

There are three important operations that trees should support: find, insert, and delete.

Find #

Finding a value in a tree uses the Binary Search algorithm.

Insert #

The insert algorithm is very similar to binary search. Here are the steps to take:

• Search for the item. If it’s found, then do nothing since the value is already in the tree.
• If it’s not found (search would return null in this case), then create a node and put it where it should be found. If using recursion, this last step is already done- all we need to do is return a new node!

Here’s the algorithm:

public BST insert(BST T, Key sk) {
    if (T == null) {
        // Create new leaf with given key. Different from search
        return new BST(sk, null, null); 
    }
    if (sk.equals(T.key)) {
        return T;
    } else if (sk < T.key) {
        T.left = find(T.left, sk); // Different from search
    } else {
        T.right = find(T.right, sk); // Different from search
    }
}

Delete #

This one’s a bit trickier because we need to make sure that the new tree still preserves the binary search tree structure. That means that we might have to shuffle around nodes after the deletion. There are three cases:

A) The node to delete is a leaf. This is an easy case- just remove that node and you’re done!

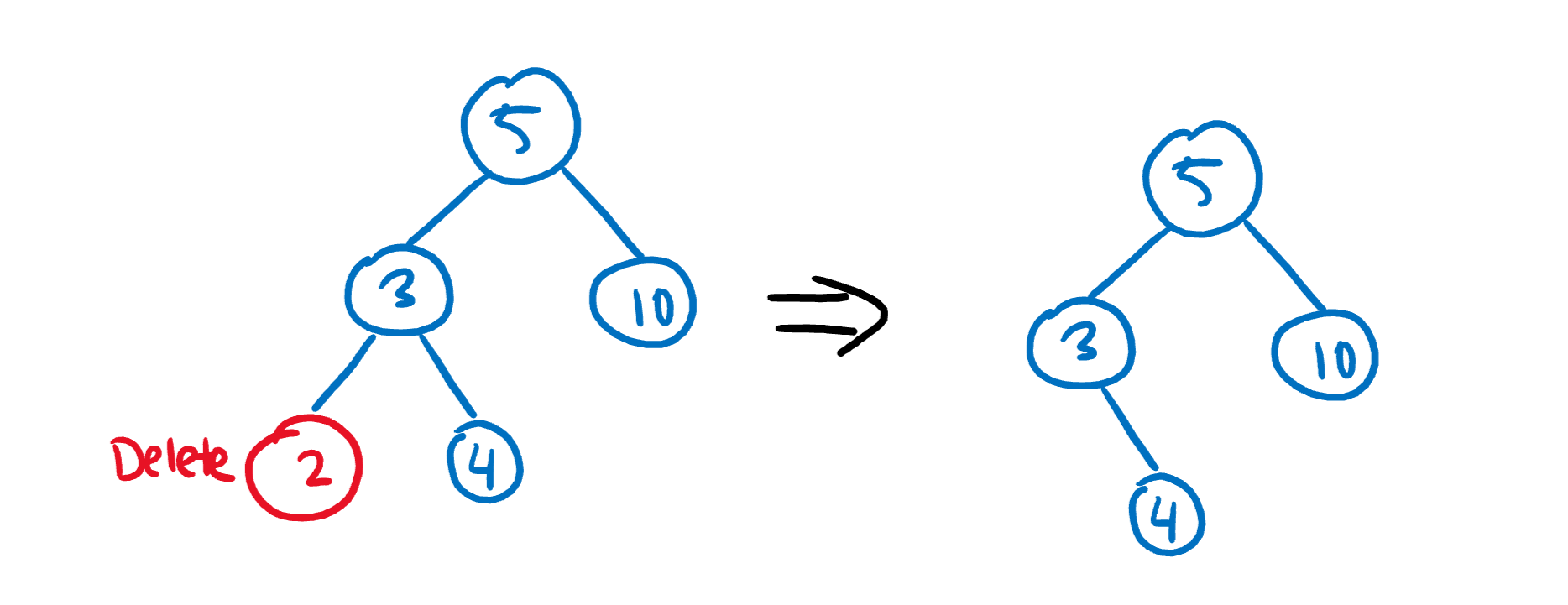
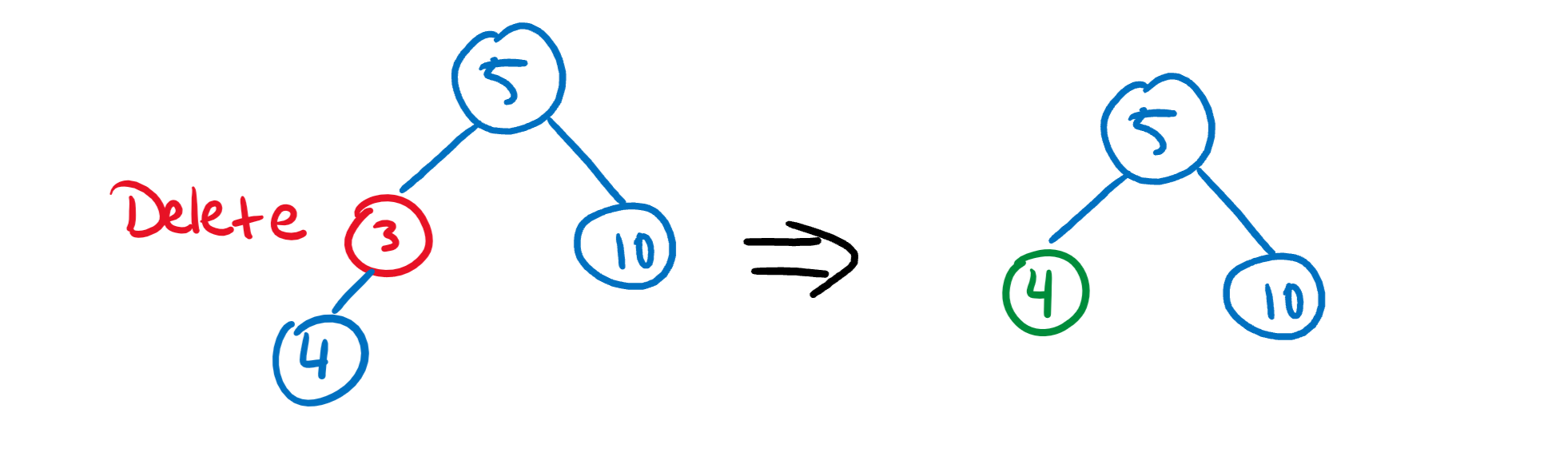
B) The node to delete has one child. In this case, swap the node with its child, then delete the node.

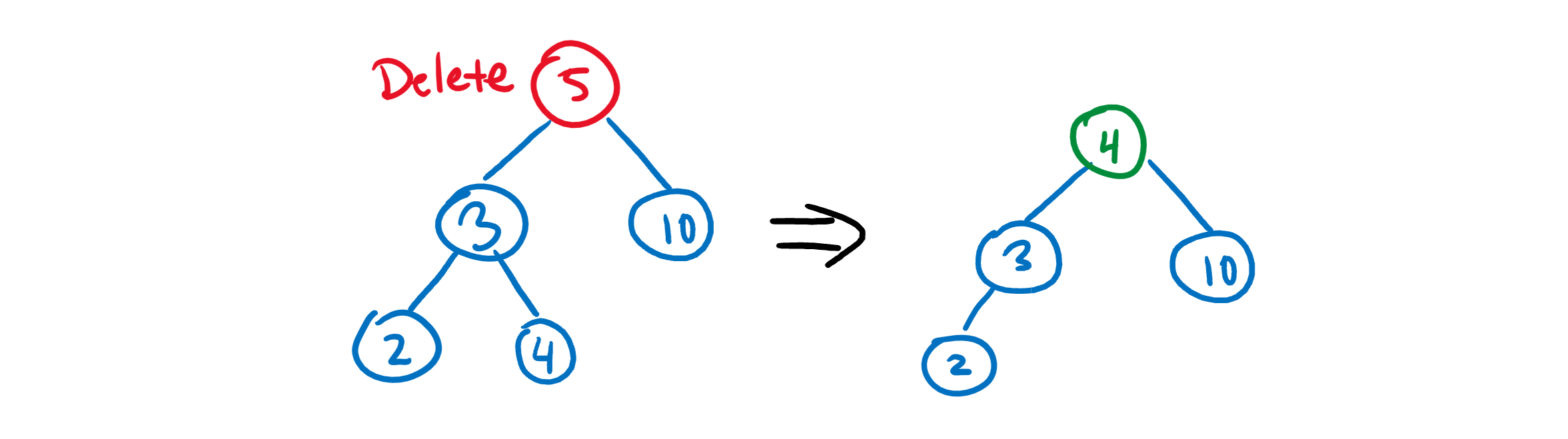
C) The node to delete has two children. This one’s trickier, because we still need to preserve the tree structure! In this case, we have to traverse the node’s children to find the next biggest value and swap that up to replace the old node.

Asymptotic Analysis #

A binary tree can be bushy or spindly. These two cases have dramatically different performances!

Bushy trees are the best case. A tree is bushy if every parent has exactly 2 children.

A bushy tree is guaranteed to have a height of $\Theta(\log(n))$ which means that the runtimes for adding and searching will also be $\Theta(\log(n))$ .

Spindly trees are the worst case. A tree is spindly if every parent has exactly 1 child. This makes the tree essentially just a linked list!

A spindly tree has a height of $\Theta(n)$ which means that the runtimes for adding and searching will also be $\Theta(n)$ .

In Balanced BSTs, we will explore ways of guaranteeing that a tree is bushy!

Limits of Trees #

While trees are extremely versatile and fantastic for a variety of applications, trees have some limitations that make it difficult to use in some situations.

• All items in a tree need to be comparable. We can’t construct a binary tree out of categorical data, like models of cars, for example.
• The data must be hierarchical. If data can be traversed through in multiple ways, or forms loops, Graphs are probably better.
• The best case runtime is $\Theta(\log(n))$ . This might seem good, but other data structures like Tries and Hash Tables can be as good as **** $\Theta(1)$ !

Tree Traversals #

Check out these pages for information on how to go through each element of a tree!

Depth First Search

Breadth First Search