Balanced Search Structures
Content Note
Please read Binary Trees before continuing!
Balanced Binary Search Trees are an even more specific subcategory of binary trees that have an important property: they are always bushy.
B Trees (2-4 Trees) #
The basic idea: Nodes can hold multiple values now! When nodes have too many values, we will split it.
A 2-4 tree is named such because each parent can have 2 to 4 children. Another constraint we will put on is a limit on the number of items allowed in a single node, so that we can guarantee that searching a single node will always be $\Theta(n).$
Adding Values to a B-Tree #
Adding values to a B Tree can be a bit tricky because we need to make sure all the properties are still followed. Here are some example scenarios:
If a node already has 2 or more children, place the new value in one of its existing children.
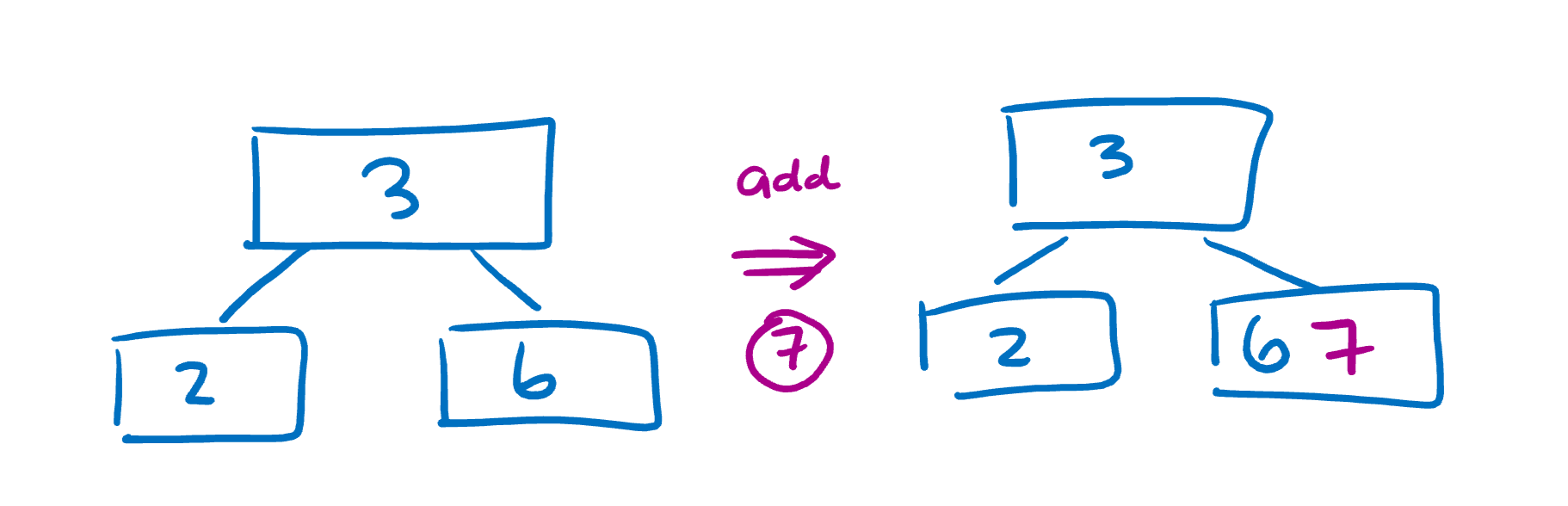
If a node is full (reaches the limit), we must split the node by moving one value up to the parent and creating another child node. Here, we’ll use a limit of 3.
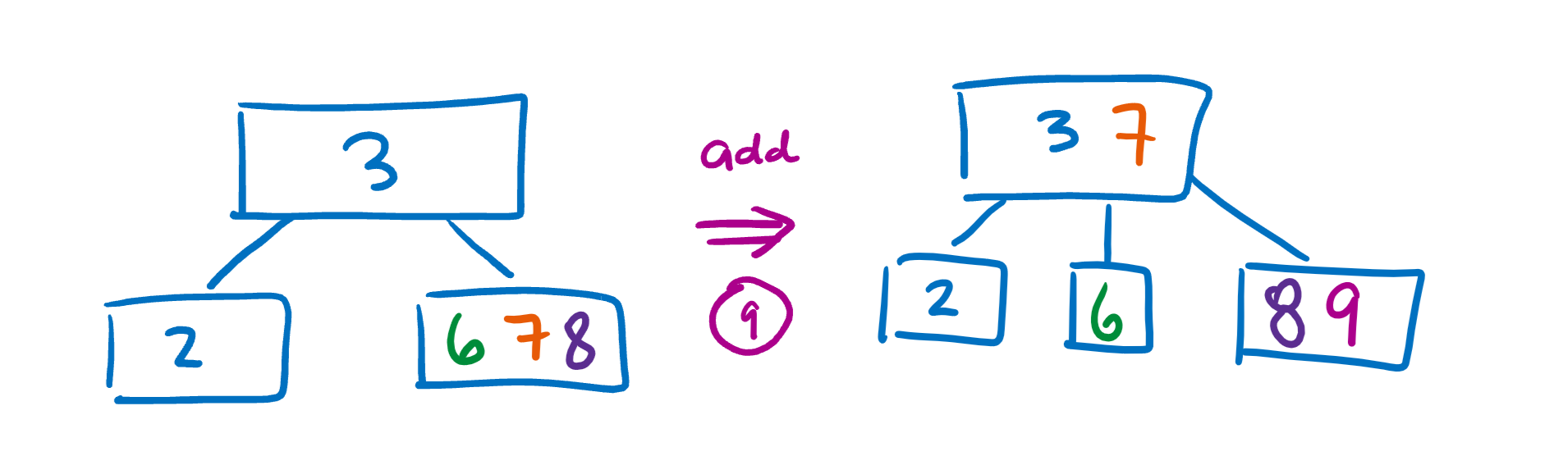
Properties of B Trees #
- Searching in a single node is constant runtime since the limit is a constant.
- All leaves must be the same distance from the root.
- A non-leaf node with k items must have k+1 children.
- The height of a B tree is guaranteed to be $\Theta(\log(n))$ because it is bushy.
Red-Black Trees and Tree Rotation #
The basic idea: Let’s try to represent B trees in a binary tree format. That means that every parent can only have 2 children! In order to do this, we’ll add an extra color property to each node.
Black nodes are just like any normal binary tree node, but Red nodes represent the nodes in B Trees that have more than one value. For example, let’s convert the B Tree we were working with before into a RB Tree.
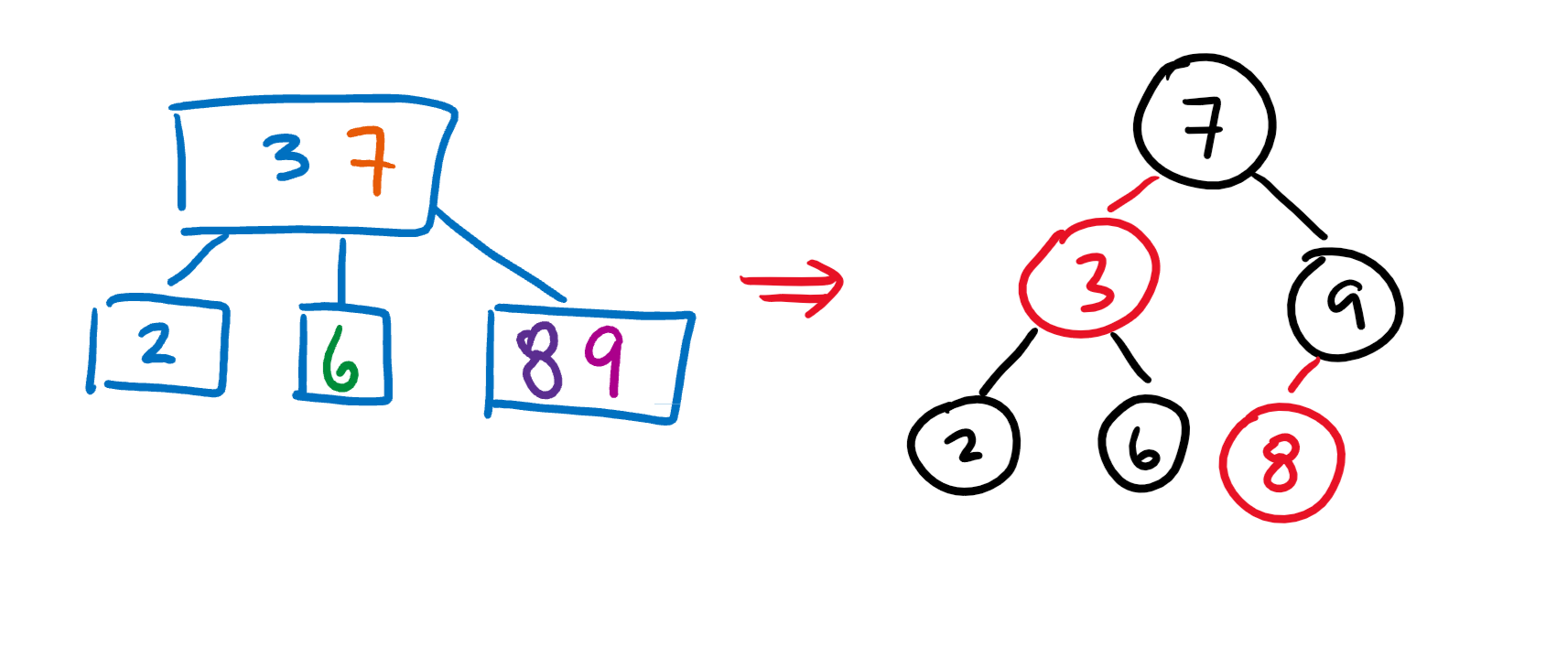
In order to make our lives easier, we’ll restrict our Red Black trees into left leaning red black trees which can only have red nodes on the left.
Tree Rotation #
In order to ensure that adding new nodes won’t break the Red Black Tree structure, we will use a concept called tree rotation which swaps around nodes. There are two rotations, a left rotation and a right rotation, which move a child node up to replace its parent. For example, a left rotation moves the right node up and left to replace the parent.
A “left rotation on 7” looks like this:
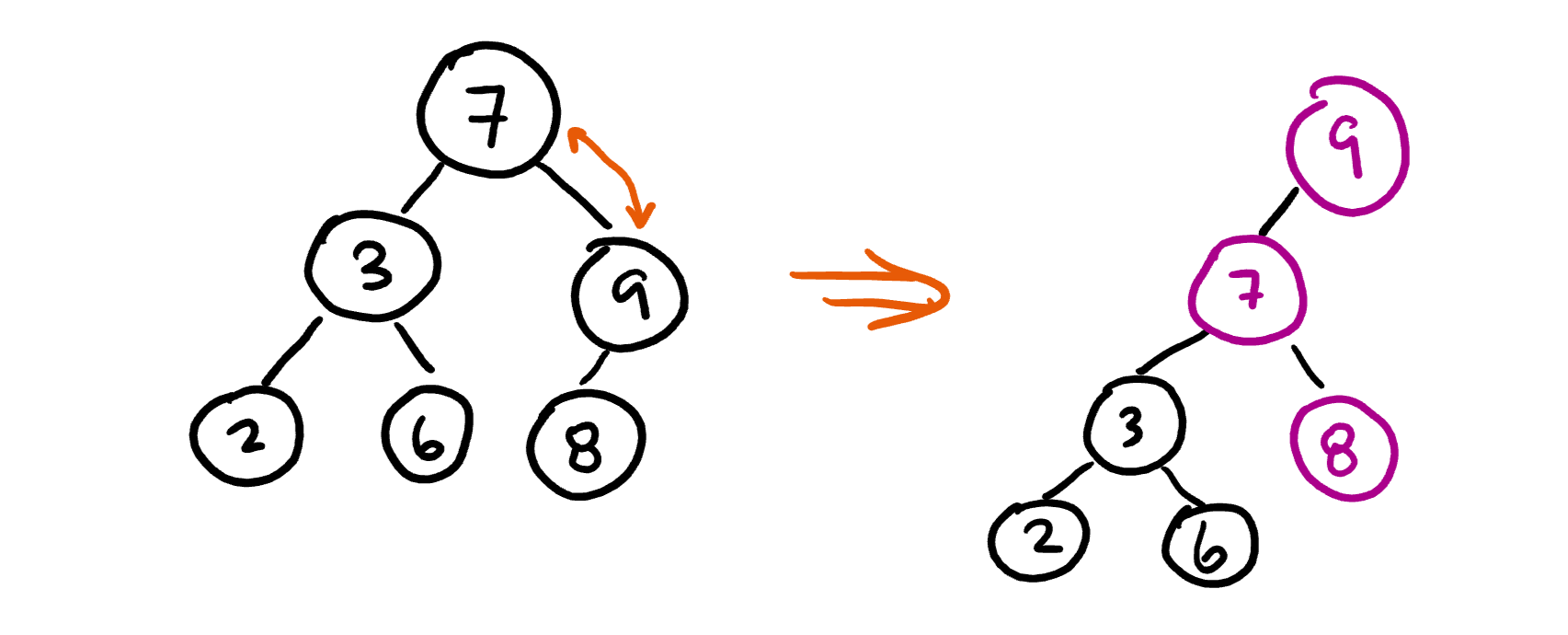
Notice that the 8 gets moved to be a right child of 7 after the rotation! This is necessary to preserve the binary tree structure.
A “right rotation on 7” looks like this:
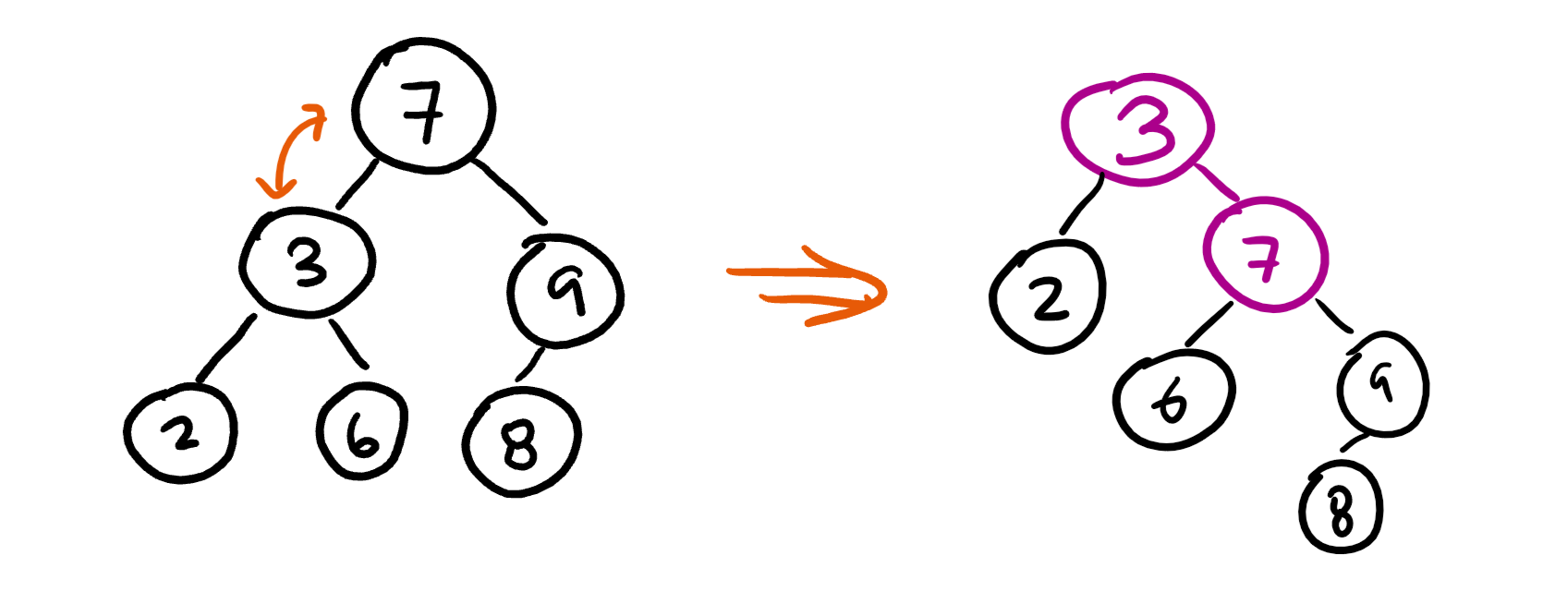
Here, the 6 gets moved to be a left child of 7.
If you want to see how these rotations can be implemented into the insert algorithm,
try the homework on implementing a LLRB Tree! Below is a brief outline on how insert works:
- Always add values to a leaf node as a red node first. Follow normal sorted binary tree rules.
- If the link is leaning right, rotate the tree to make it left leaning.
- If a node already has a red link to the left, temporarily add it to the right also as a red link.
- Then, flip the color of all links connected to the node (if previously black, turn red; if previously red, turn black)
- Might need to fix right-leaning red nodes that are created as a result
- If a node has red links to both parent and child, rotate it such that it becomes the above case, and then handle that case like you did before.
Properties of Red Black Trees #
Like B Trees, Red Black Trees have some important properties that allow them to be easily distinguishable.
- Red Black trees have a one-to-one correspondence with B trees. That means for every Red Black tree, there is exactly one B Tree that represents the same connections. This also means that a Red Black Tree will have the same runtimes as their corresponding B Trees. (Take a linear algebra course to learn more about isomorphisms 🙂 )
- Every node must have the same number of black nodes in between itself and the root. This might be a bit surprising at first, but remember that their corresponding B Tree is always bushy, and red links mean a multi-value node in a B Tree.