Graphs

Introduction #

Graphs are simply a collection of vertices connected by edges. They’re very similar to trees, but are much more versatile and don’t require hierarchical relationships like trees do.

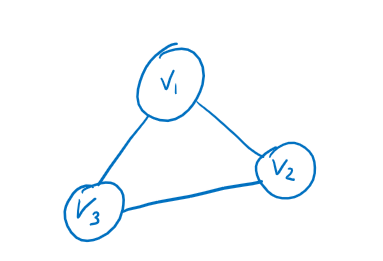
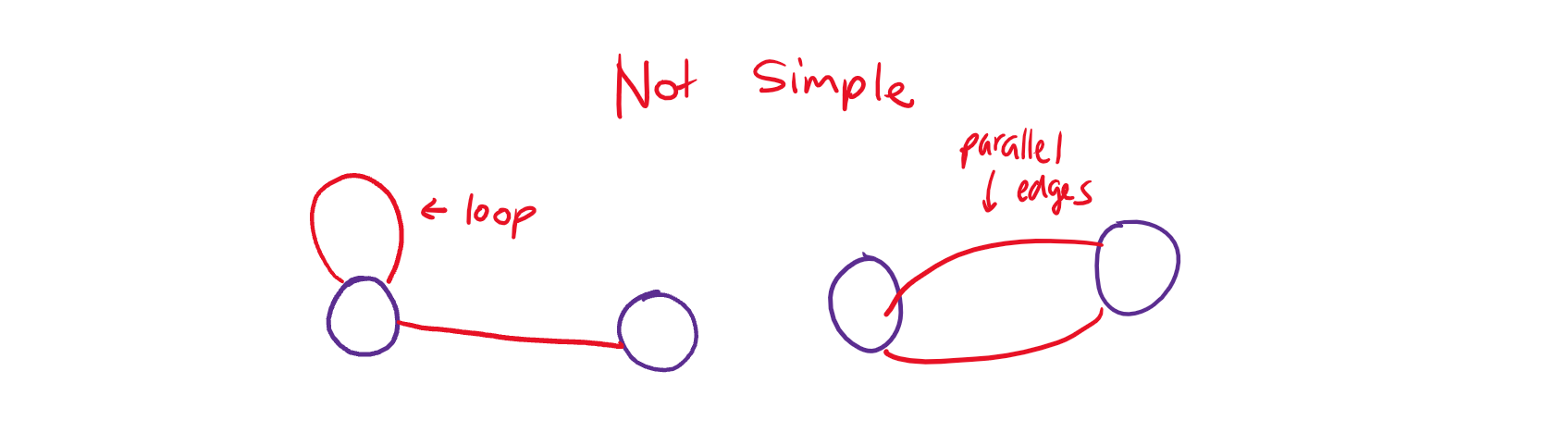
For most purposes, we will be working with simple graphs that follow two rules:

• There are no loops (a connection of a node to itself).
• There are no parallel edges (two edges that connect the same two vertices).

Graph Properties #

Graphs can be described by some properties that they could have. Here are the important ones:

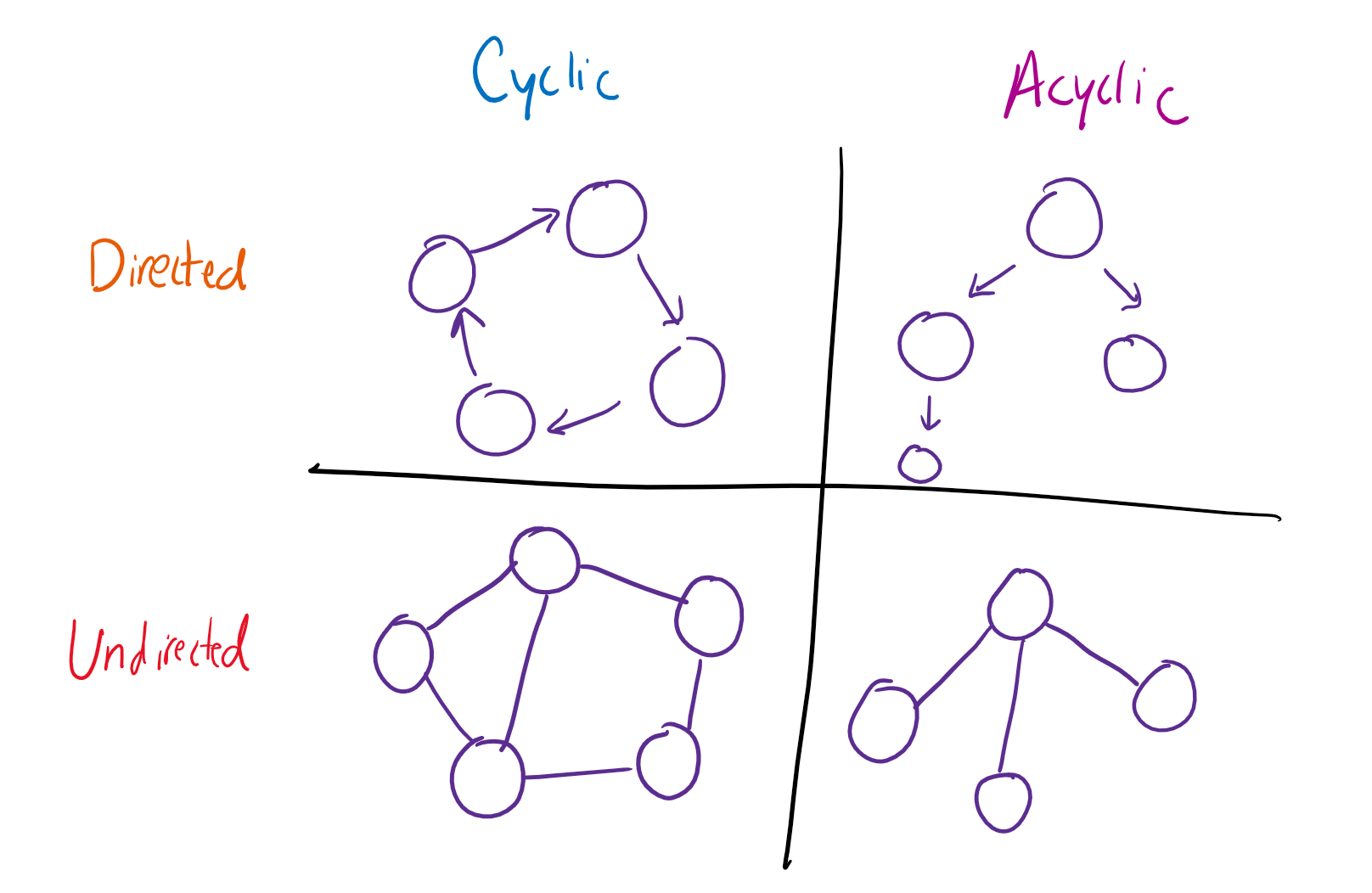
A graph can be directed if edges are arrows and have a direction, or undirected if you can cross edges in any direction.

A graph is cyclic if the edges form a loop, or acyclic if there are no loops (like in a tree).

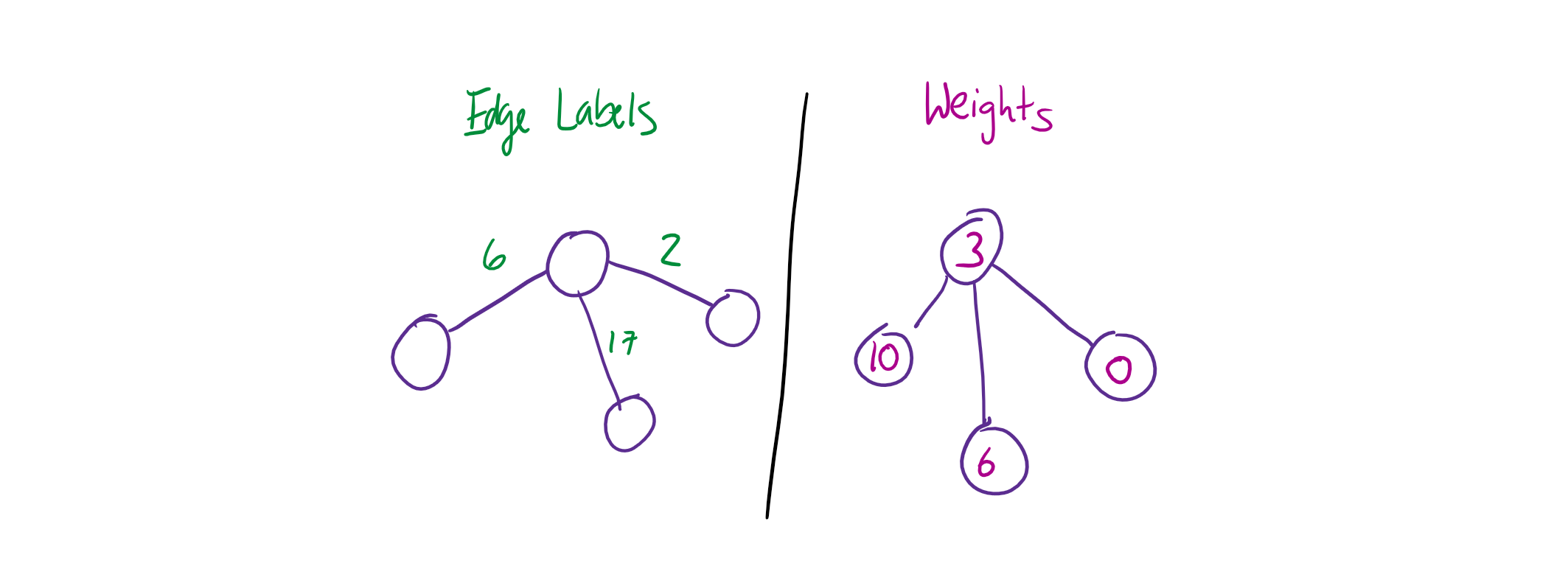
Graphs can have edge labels if edges are numbered (great for distances). They can also have vertex weights if vertices are numbered (great for priorities or costs).

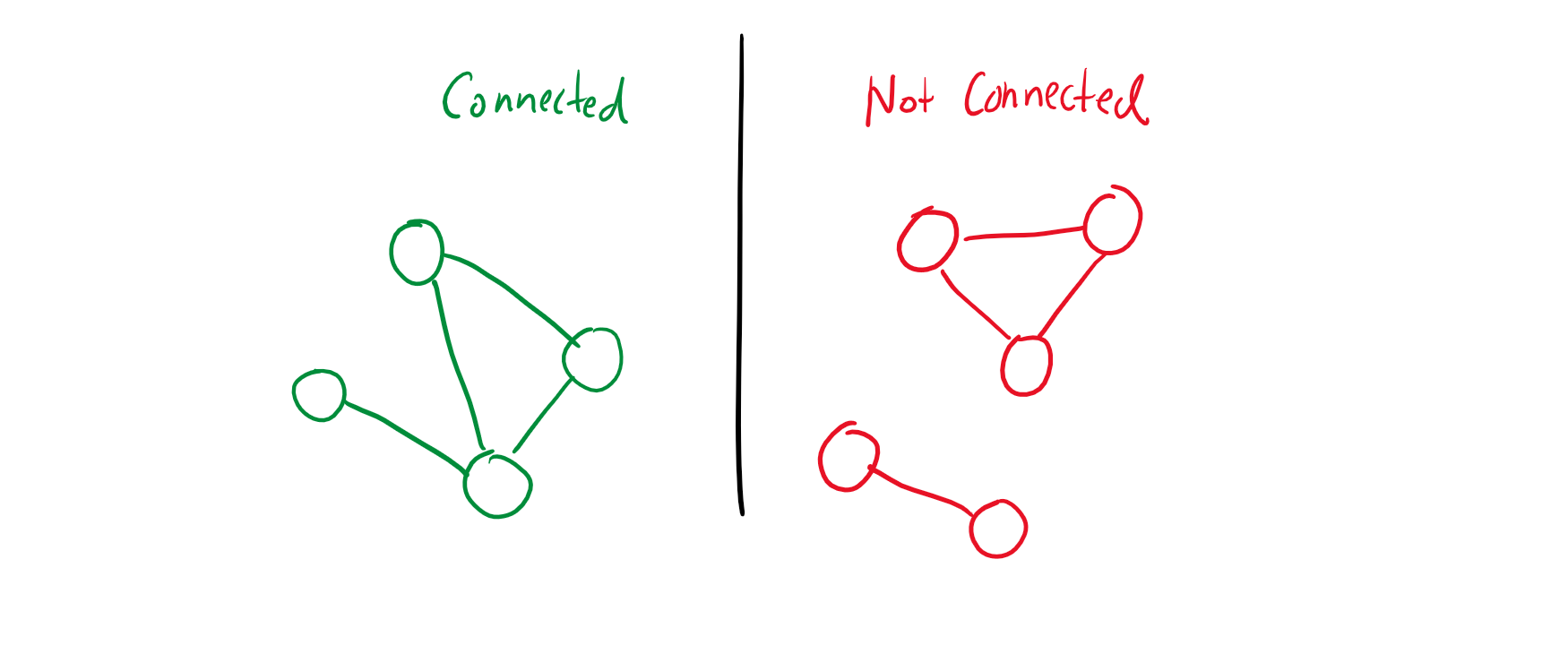
Graphs are connected if all of the vertices are connected with edges, such that you can freely move from one vertex to any other vertex.

Graph Queries #

Here are some cool things you can do with graphs:

• Is there a path between two vertices? (s-t path)
• What is the shortest route between two vertices? (shortest s-t path)
• Are there cycles? (cycle detection)
• Can you visit each vertex/edge exactly once? (Euler tour / Hamilton tour)
• Is a graph connected? (connectivity problem)
• Is a vertex that disconnects the graph when removed? (single point of failure / biconnectivity)
• Are two graphs isomorphic?
• Can a graph be drawn with no crossing edges? (planarity)

More on Graphs #

Depth First Search (DFS), Breadth First Search (BFS), Minimum Spanning Trees, Shortest Paths, Dijkstra’s Algorithm, A* Search, Prim’s Algorithm, and Kruskal’s Algorithm all rely on graphs. Graphs are a super useful concept!!!