Amortization
Amortization #
Content Note
Please read Asymptotic Analysis Basics first. If you don’t, none of this will make any sense!
Amortization means spreading out.
Sometimes, an operation takes different amounts of time for different values of $n$. Rather than having to report runtimes for each different case, we can instead average all of them out and report the amortized runtime.
This is especially good for functions where most actions have a low cost, but a few have a high cost. We’ll see an example of this further down the page!
A Case Study: Resizing Arrays #
As you probably know, normal Java arrays don’t resize. If we create a new int[5] then that array will always have a length of 5.
But what if we wanted to make an array resize itself every time it reaches capacity? (Like a List!) Let’s see what happens when we add one to the array size:
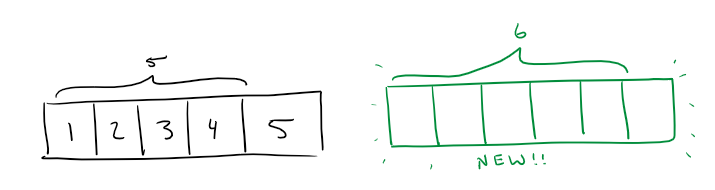
First, we have to make a new array with a new size:
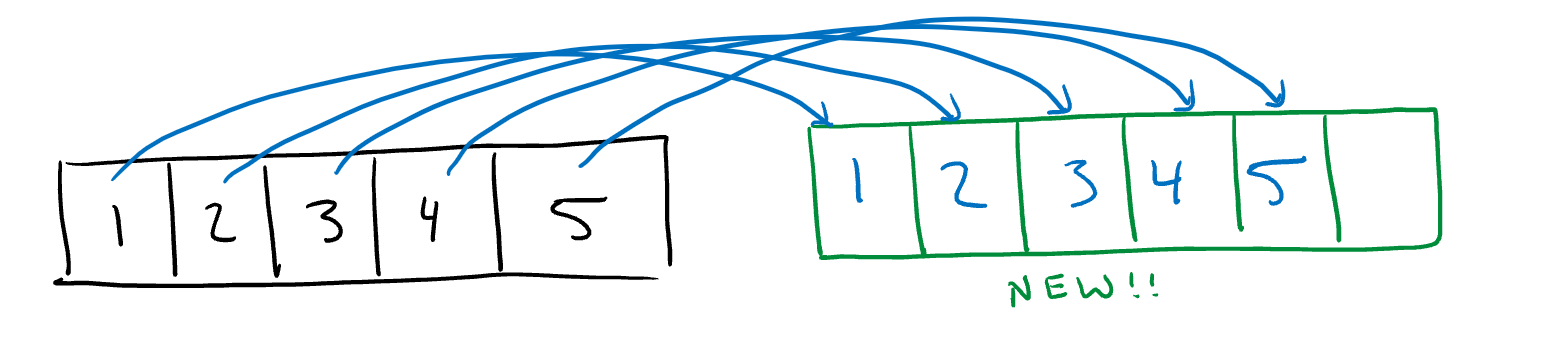
Then, we have to copy over all of the old elements over:
Finally, we can add in the new element!
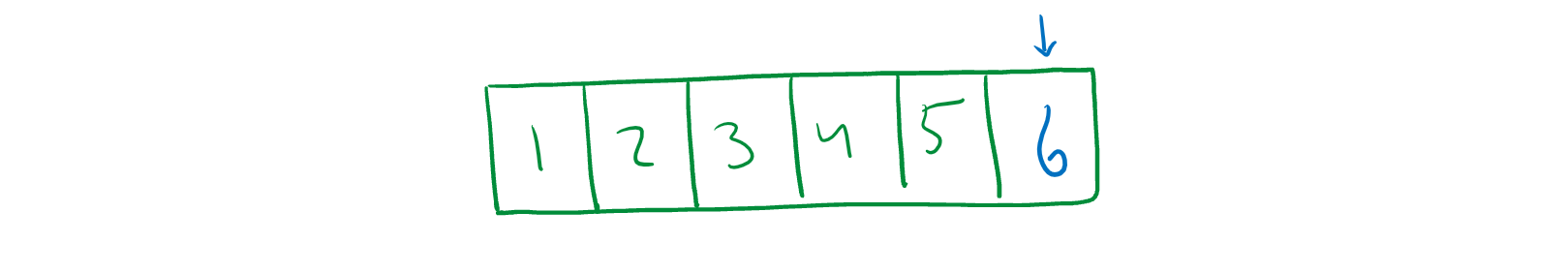
Let’s analyze the runtime of this operation.
- A single resizing will take $\Theta(n)$ time.
- Adding a single element will take $\Theta(1)$ time.
- Together, a single operation will take $\Theta(n+1)$ time, which simplifies into $\Theta(n)$ .
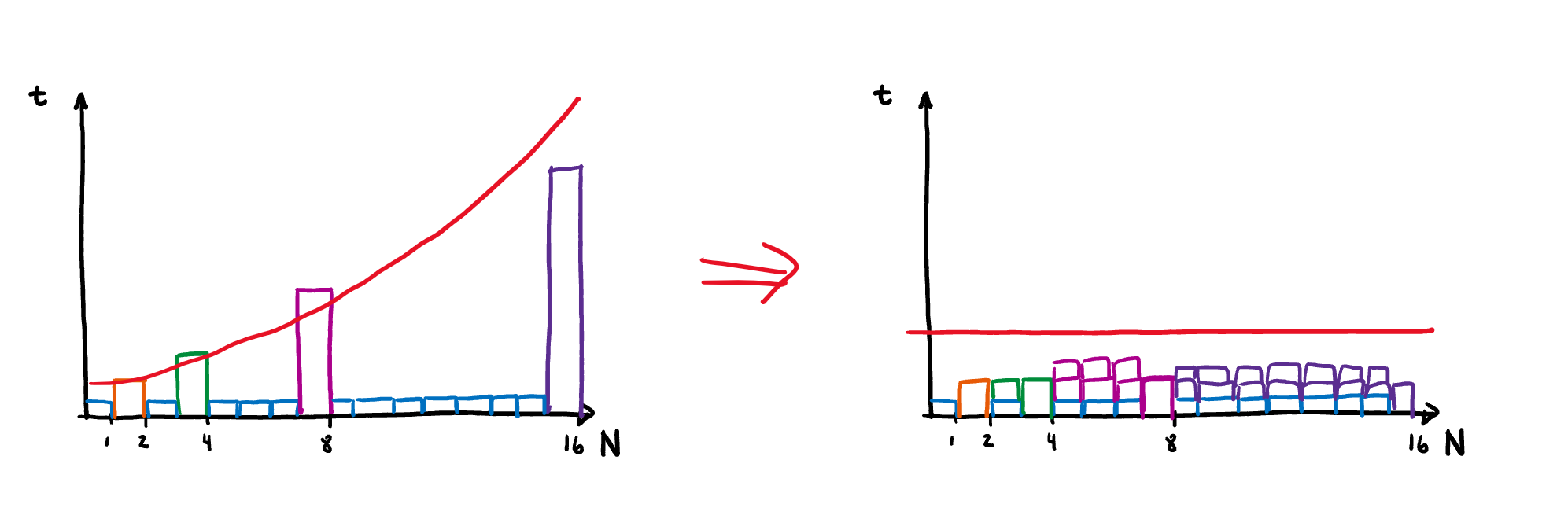
- Since we’re doing a n-operation n times, the end result is a resizing function that is$\Theta(n^2)$. We can do better with the power of amortization!
What if we doubled the size instead of adding one? #
- A single resizing will take $\Theta(2n)$ time _**_which simplifies into $\Theta(n)$ time.
- We do this every time the array hits a power of 2 (2, 4, 8, 16, 32 …).
- Adding a single element will take $\Theta(1)$ time.
- We do this every time we add a new element, so in all we add n elements. Therefore, this is an
- $\Theta(n)$operation.
- We do this every time we add a new element, so in all we add n elements. Therefore, this is an
Therefore, the unsimplified function is: $\Theta(n + (2 + 4 + 8 … +2^i))$ where $2^i$ is the largest power of two less than n. This might not seem clear on its own, so let’s rewrite it:
$ \theta(n + (\frac{n}{2} + \frac{n}{4} + … + 8 + 4 + 2)) $
Intuitively, this looks like this:
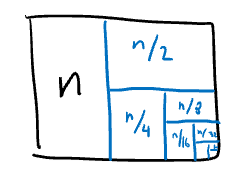
Mathematically, it looks like this:
$ n + n\sum_{n=1}^{n}(\frac{1}{2})^n $
Which simplifies to $2n$if you recall your power series properties . Therefore, this approach is $\Theta(n)$ !!