Kruskal's Algorithm

Content Note

Before reading, review Minimum Spanning Trees and Union Find (Disjoint Sets)

Union Find (Disjoint Sets)

Union Find (Disjoint Sets) Content Note > This is not a complete entry, because I feel like existing course materials already cover...

11/19/2023

as they both make Kruskal’s algorithm possible!

Conceptual Overview #

Kruskal’s algorithm is another optimal way to construct a minimum spanning tree. It’s benefits are that it is conceptually very simple, and easy to implement. The idea is that first we sort all the edges of the graph in order of increasing weight. Then, add the smallest edge to the MST we are constructing unless this creates a cycle in the MST. Repeat until V - 1 edges total.

Detailed Breakdown #

In order to optimally check if adding an edge to our MST creates a cycle, we will use a WeightedQuickUnion object. (See Union Find (Disjoint Sets)

To run the algorithm, we start by adding all the edges into a PriorityQueue

Let’s see an example of Kruskal’s Algorithm in action!

Here, we start with a simple graph and have sorted all of its edges into a priority queue.

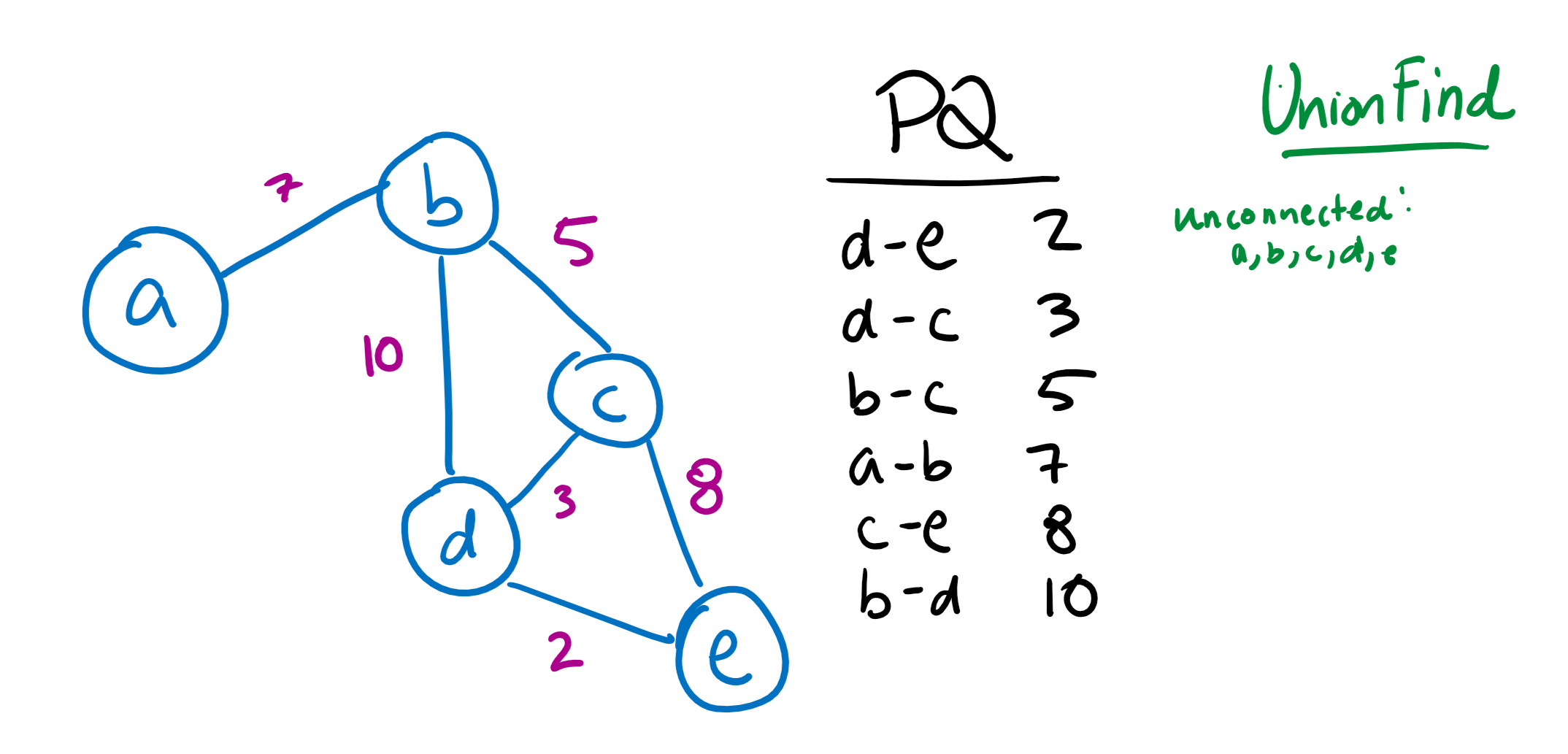
Since the edge DE is the shortest, we’ll add that to our UnionFind first. In the process, we’ll remove DE from the priority queue.

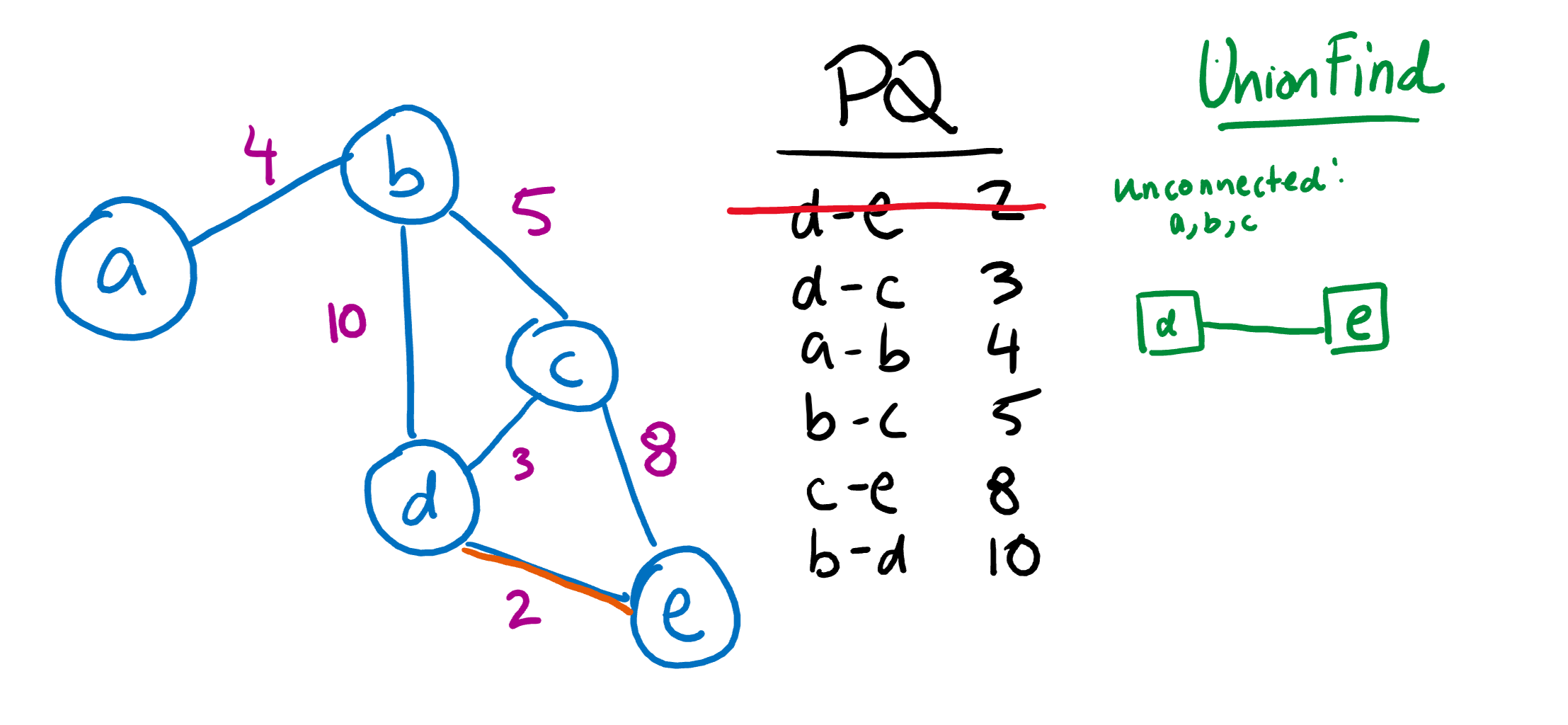
We’ll do the same thing with the next shortest path, DC.

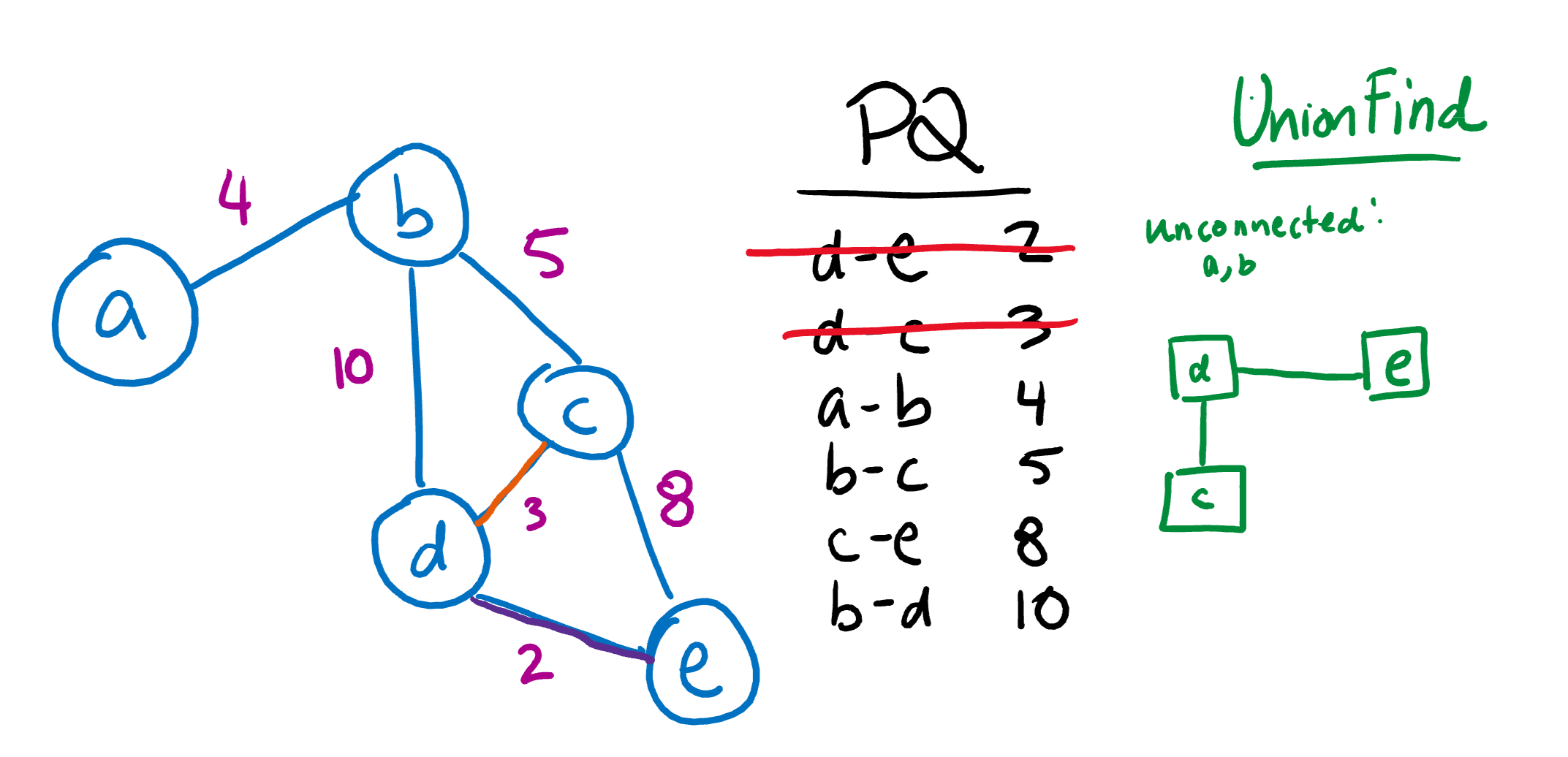
Now, let’s move on to AB. Notice that this time, connecting A and B creates another disjoint set! Unlike Prim’s Algorithm, Kruskal’s Algorithm does not guarantee that a solution will form a tree structure until the very end.

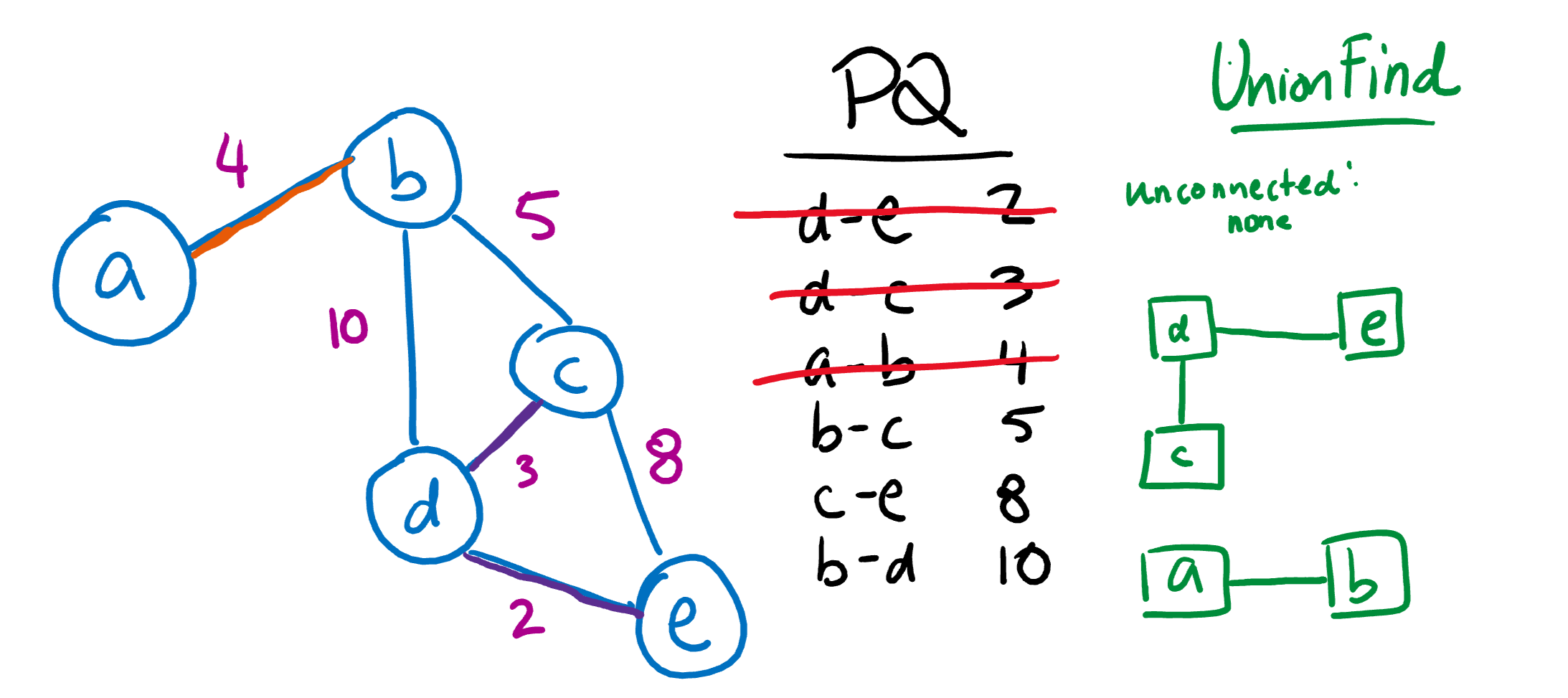
Now, let’s connect BC.

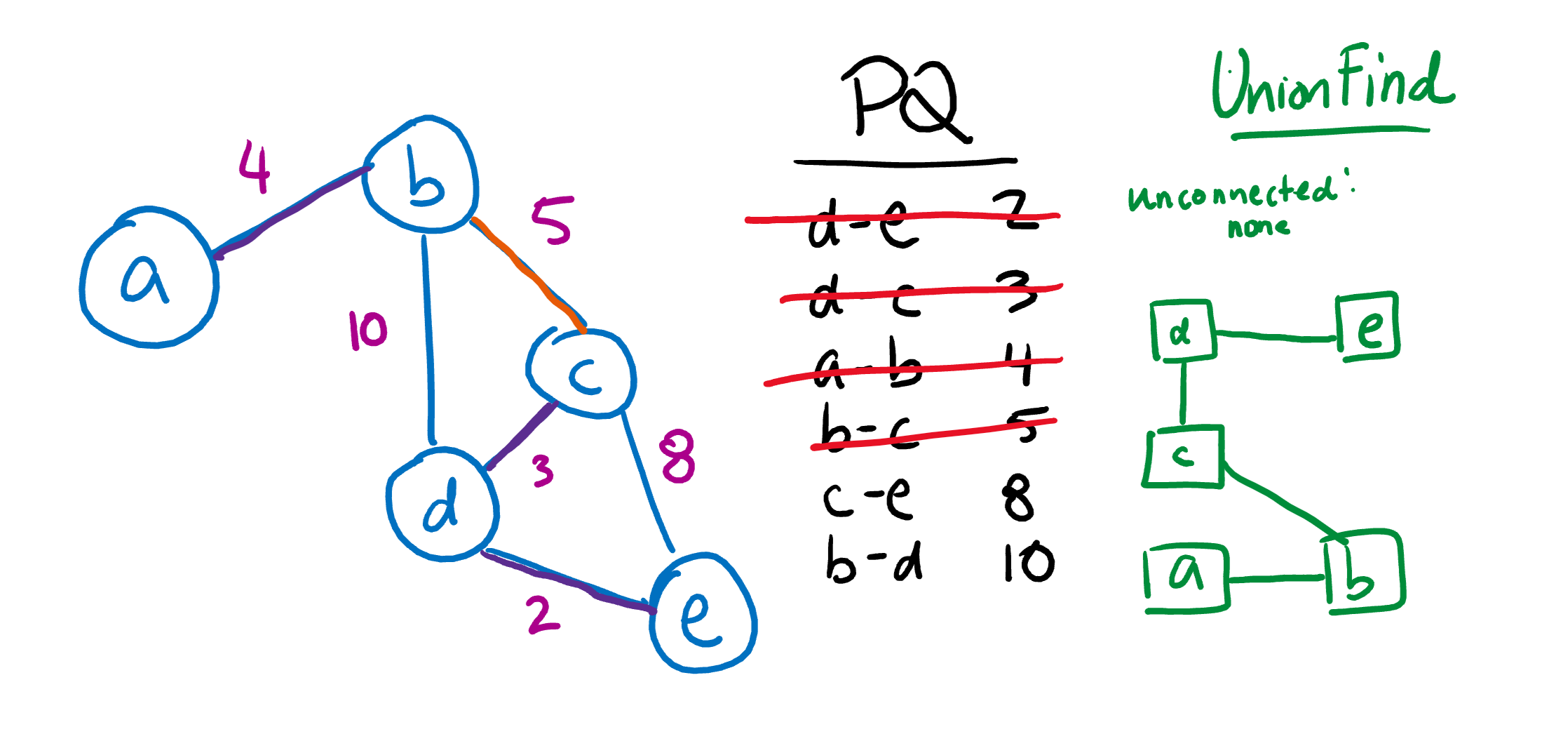
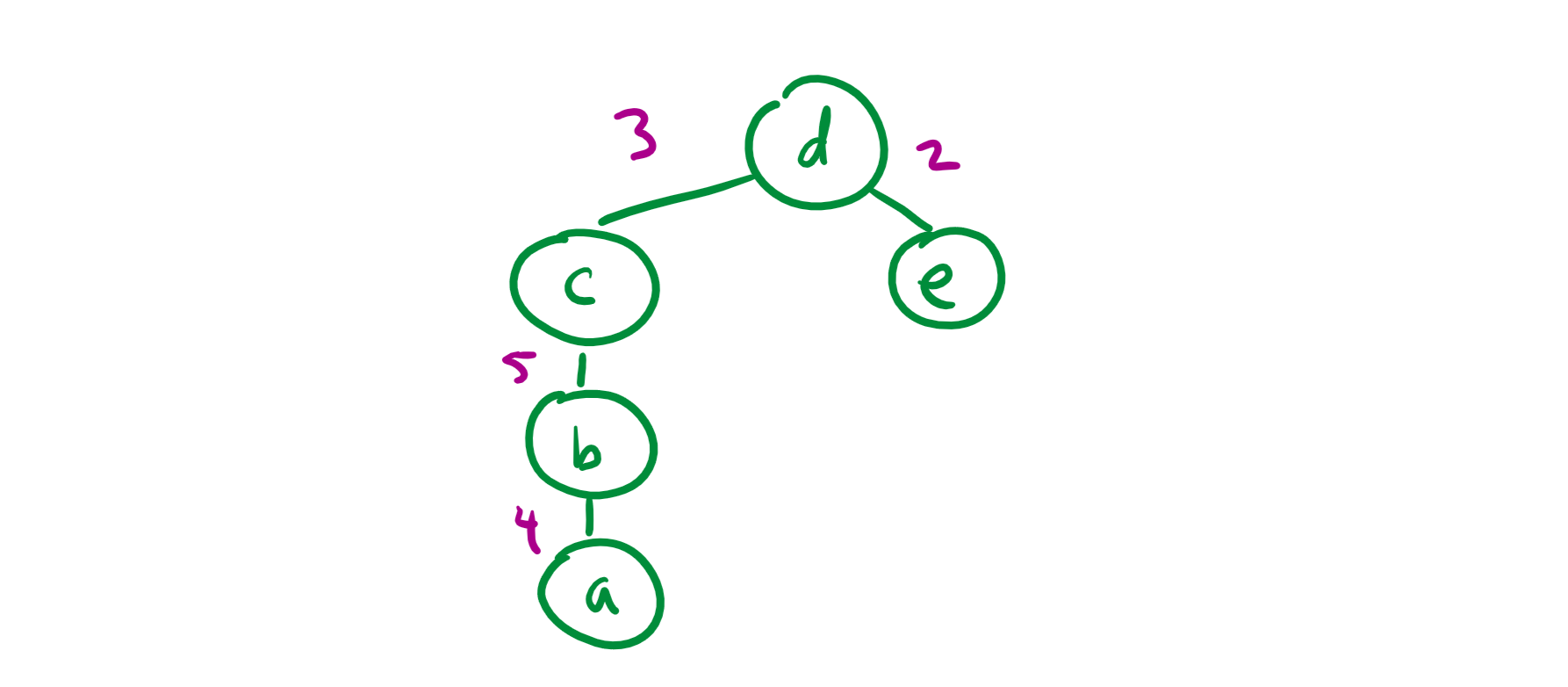
Since CE and BD would both form cycles if connected, we are done 😄 Here’s the final tree:

PseudoCode #

public class Kruskals() {

    public Kruskals() {
        PQ edges = new PriorityQueue<>();
        ArrayList<Edge> mst = new ArrayList<>();
    }

    public void doKruskals(Graph G) {
        for (e : G.edges()) {
            PQ.add(e);
        }
        WeightedQU uf = new WeightedQU(G.V());
        Edge e = PQ.removeSmallest();
        int v = e.from();
        int w = e.to();
        if (!uf.isConnected(v, w)) {
            uf.union(v, w);
            mst.add(e);
        }

    }
}

Runtime Analysis #

Left as an exercise to the reader 😉

(The answer is $\Theta(E\log(E))$by the way. Try to convince yourself why!)