Breadth First Search (DFS)

Breadth First Search (BFS), like Depth First Search (DFS)

The main difference is that BFS visits all children before any subgraphs. In a tree, we call this level order.

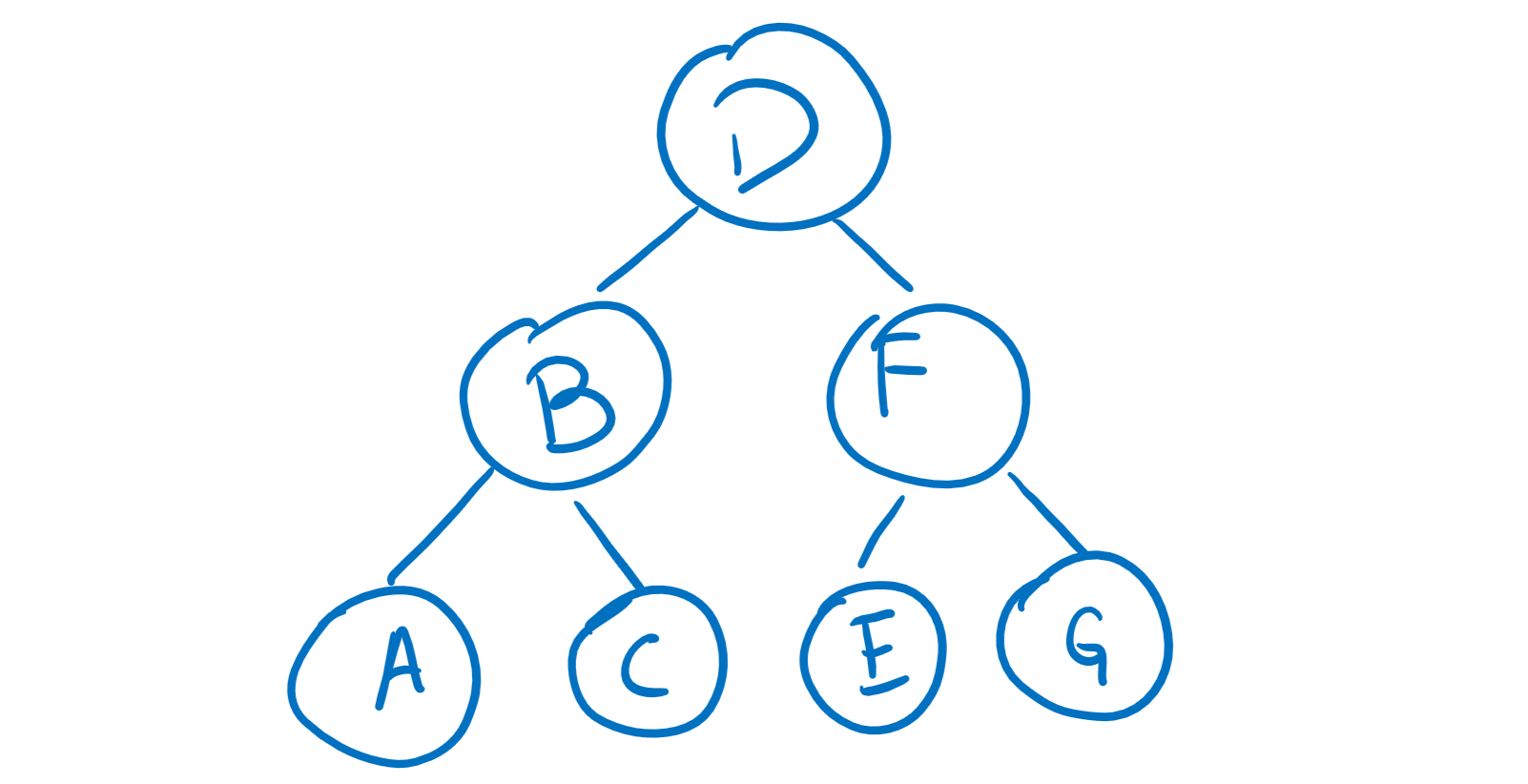
For the example tree above, a level order traversal would go in this order: D B F A C E G.

Step by Step #

Let’s see how we might implement BFS.

Some data structures we will need are:

• A graph to traverse.
• A queue Q to keep track of which nodes need to be processed next.
• A list of booleans marked to keep track of which nodes were already visited.
• (Optional) edgeTo and distTo to keep track of information that might be useful for other applications (like Dijkstra’s Algorithm

  Dijkstra's Algorithm

  Content Note > Before continuing, make sure you're comfortable with Graphs, Stacks and Queues, and Shortest Paths. One sentence overview Visit vertices in...

  11/19/2023

  ).

First, let’s start with a vertex in the graph by marking it and adding it to the queue.

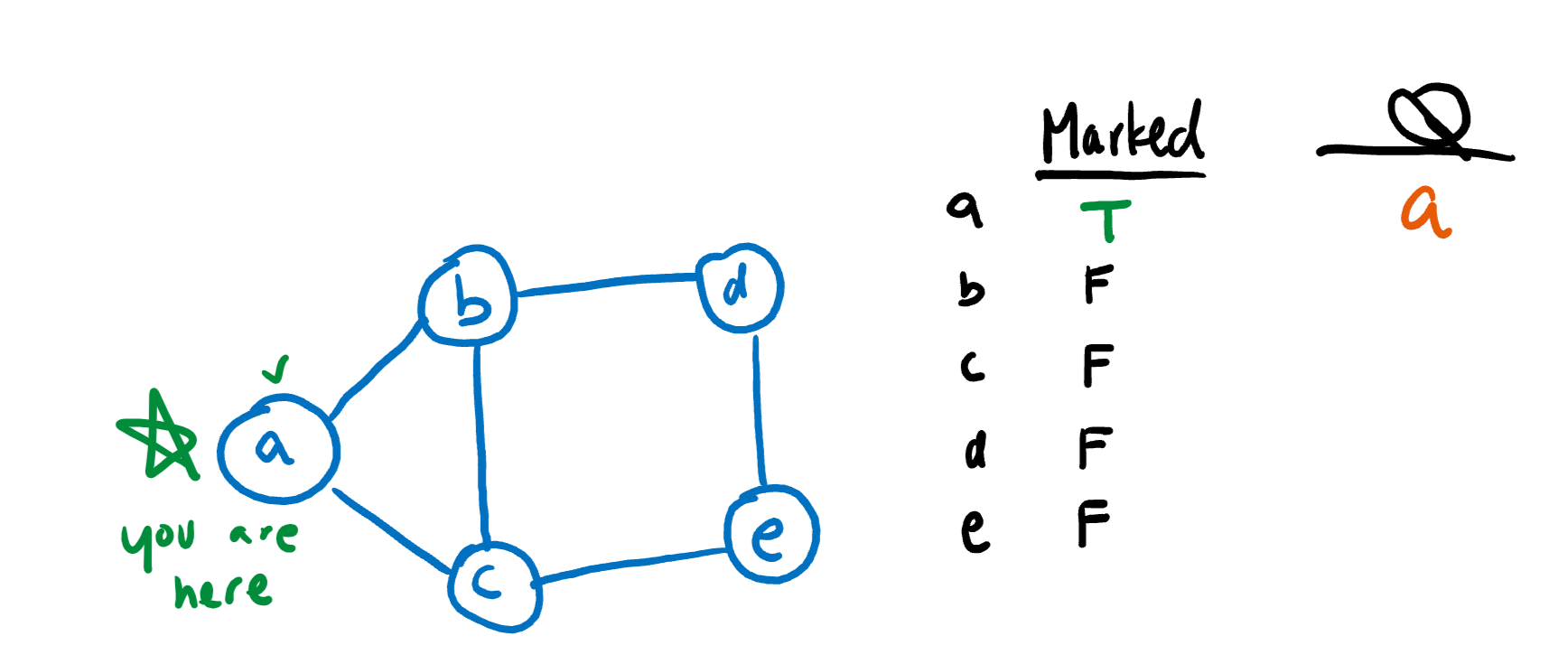
The next step is to remove A from the queue and add its children (B and C) to the queue. Also, we need to mark all of the children.

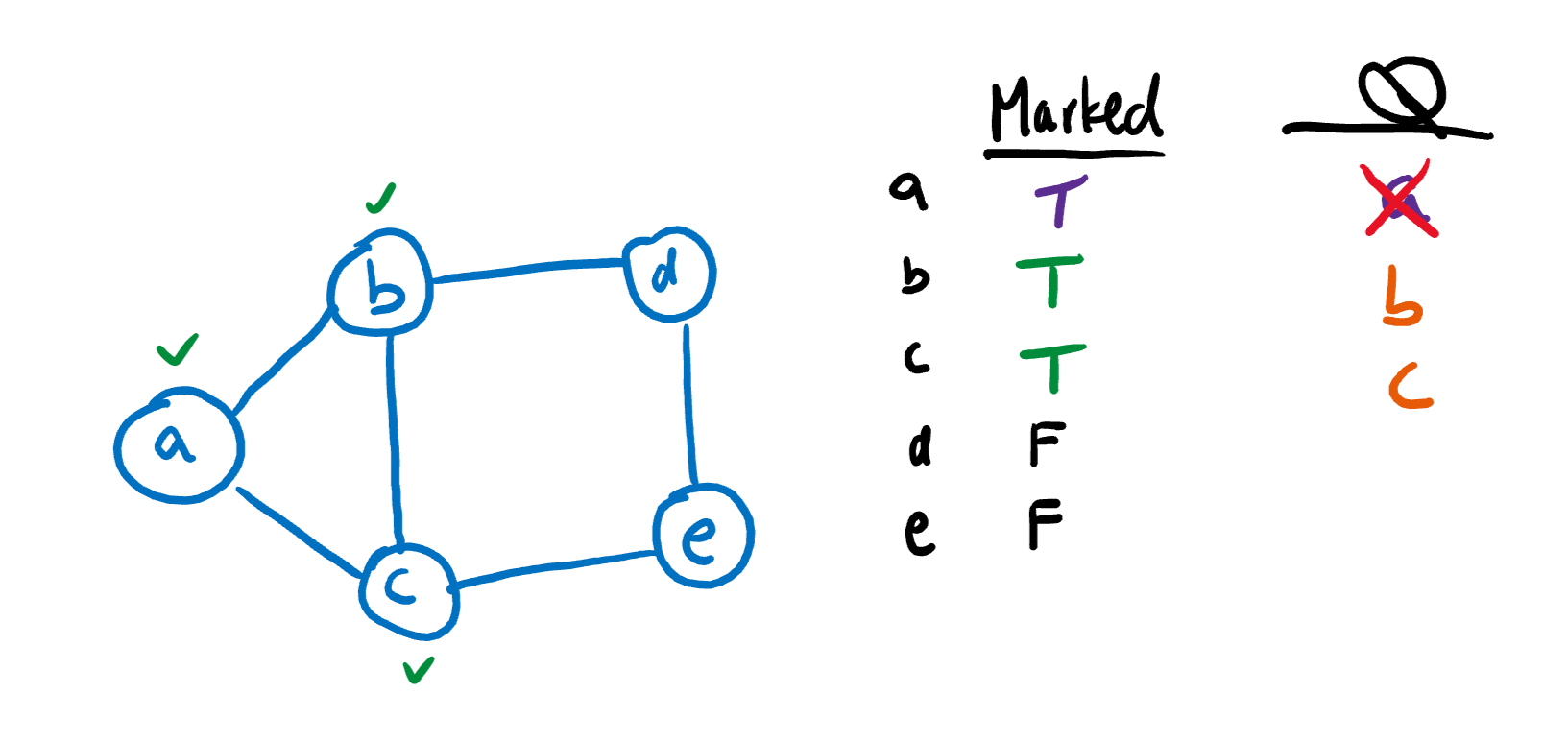
Next, we’ll move onto the next item on the queue (B). We’ll do the same thing that we did with A: remove B, mark all its children, and add its children to the queue. Since C is already marked, we do not add it to the queue again.

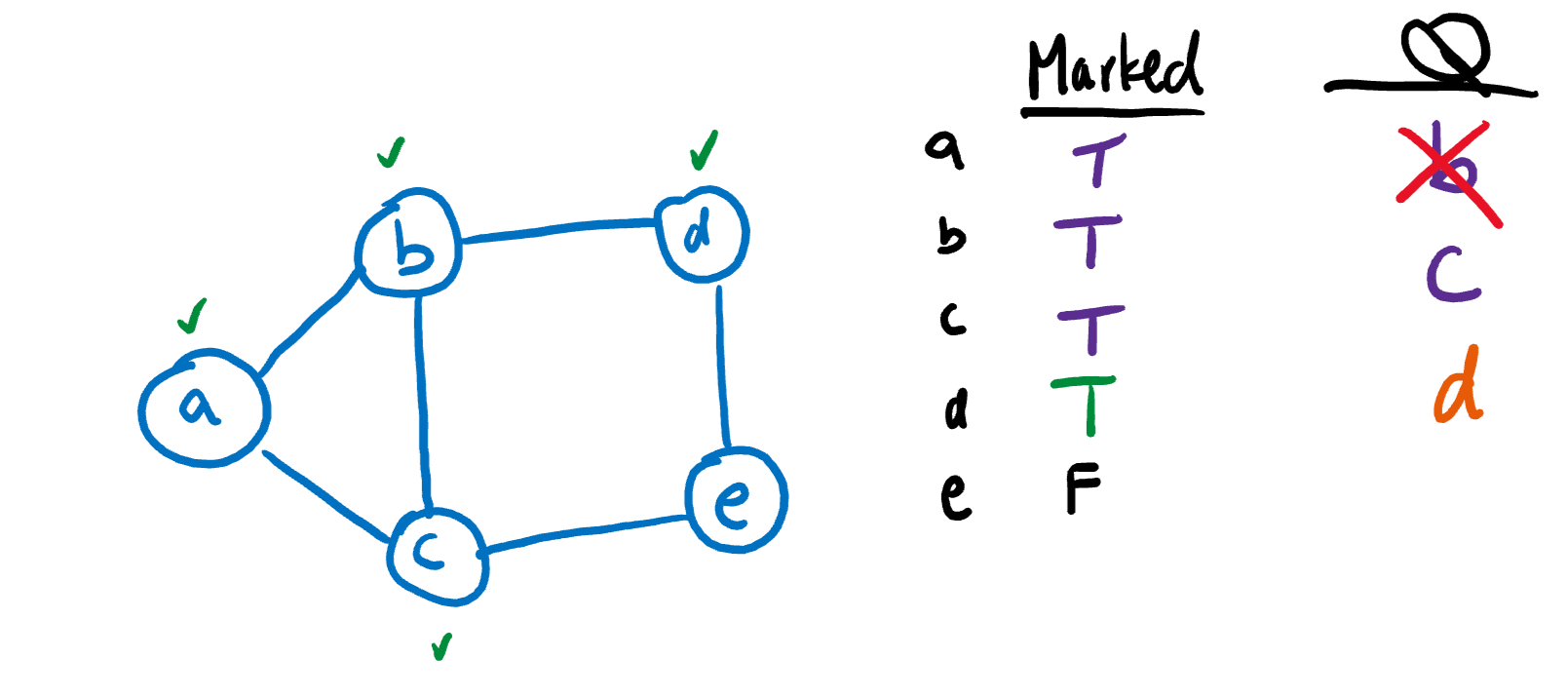
Now, we’ll move on to the next item on the queue, C, and do the same thing. Again, we won’t add C or A because they are both marked.

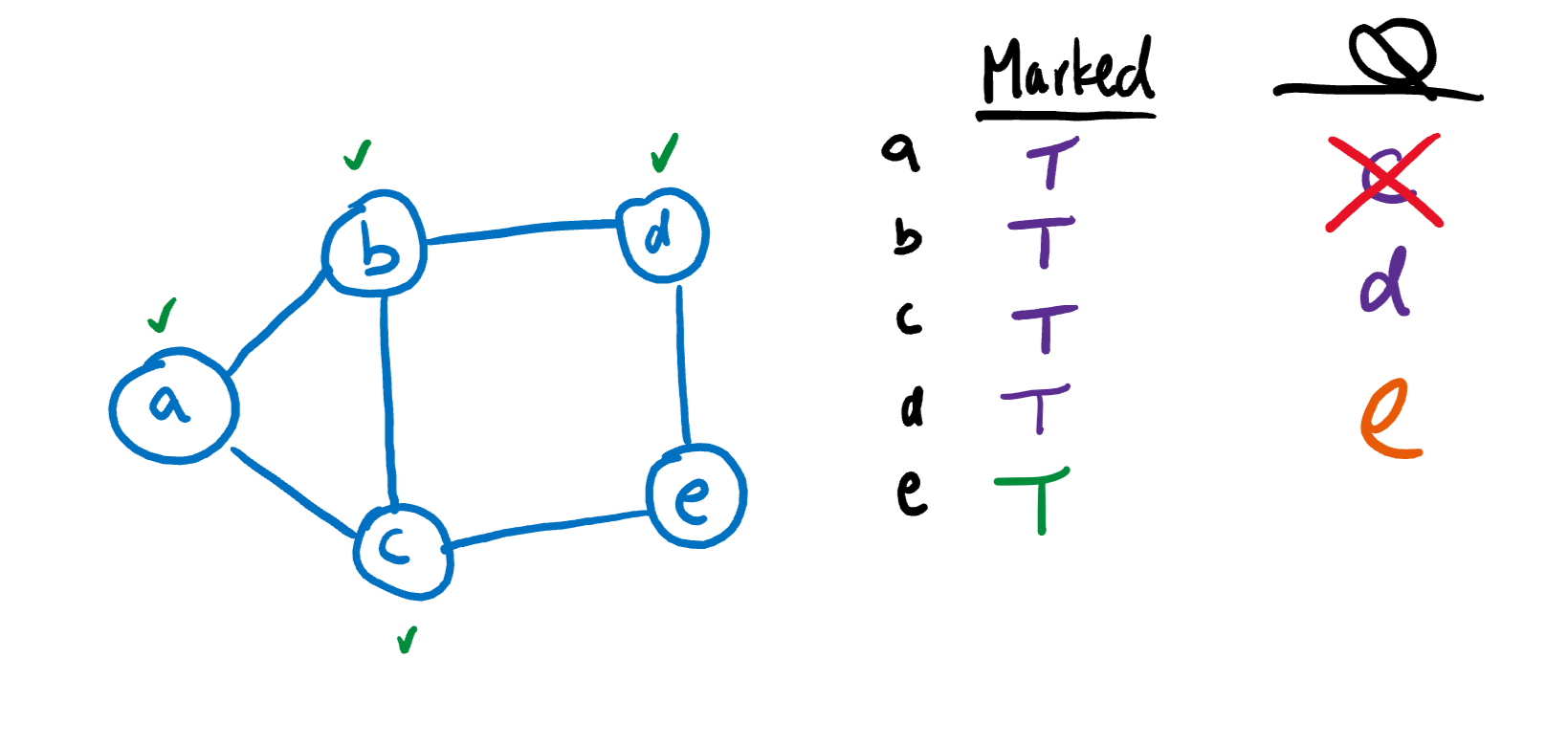
Finally, we’ll visit the two remaining nodes in the queue, D and E. Since all of the nodes are marked now, there aren’t any other nodes to visit.